


Next: 2. Funktionen auf Flächen
Up: 1. Kurven und Flächen
Previous: 1.8 Algorithmen für biquadratische
Inhalt
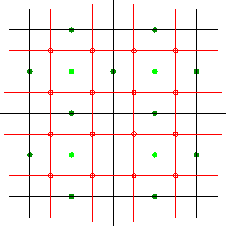
Abbildung 1.18:
Doo-Sabin-Algorithmus
 |
Liegen zwei irreguläre Polygone eines Kontrollnetzes direkt
nebeneinander oder liegt nur ein reguläres Polygon zwischen ihnen,
dann können wir an dieser Stelle den G-Spline-Algorithmus nicht
einsetzen. Um ein solches Kontrollnetz doch verwenden zu können,
müssen wir es zunächst verfeinern, indem wir die vorhandenen Polygone
durch mehrere, kleinere Polygone ersetzen.
Eine Möglichkeit hierzu bietet der
Doo-Sabin-Subdivision-Algorithmus (vgl. [Doo78]). Basierend
auf den Verfeinerungstechniken für biquadratische, uniforme
B-Spline-Flächen entwickelten Donald Doo und Malcolm Sabin einen
Subdivision-Algorithmus, der zur Verfeinerung von Kontrollnetzen
beliebiger Topologie verwendet werden kann. Die neuen Kontrollpunkte
werden dabei als Mittel von vier durch das jeweilige Polygon
bestimmten Punkten berechnet. Im folgenden sei der Kantenpunkt einer
gegebenen Kante der Mittelpunkt dieser Kante und der Gitterpunkt eines
Polygons sei das Mittel aller Punkte dieses Polygons.
Beim Doo-Sabin-Algorithmus wird das alte Kontrollnetz vollständig
durch ein neues ersetzt, wobei pro Kontrollpunkt und Polygon ein neuer
Kontrollpunkt erzeugt wird, der das Mittel vom alten Kontrollpunkt,
dem Gitterpunkt und den zwei Kantenpunkten ist. Diese Punkte werden
dann zu einem neuen Kontrollnetz zusammengesetzt, so daß jedes
ursprüngliche Polygon durch ein kleineres ersetzt wird und für jede
Kante und jeden Kontrollpunkt ein neues Viereck entsteht. Mit diesen
neuen Vierecken werden die verkleinerten Polygone miteinander
verbunden. Dieser Prozeß ist in Abbildung 1.18
illustriert. Dabei sind die ausgefüllten Punkte in der Mitte der
Quadrate die Gitterpunkte, die ausgefüllten Punkte auf den Linien sind
die Kantenpunkte und die nicht ausgefüllten Punkte markieren die neuen
Kontrollpunkte.
Algorithmus 1.3
| doo_sabin |
| Doo-Sabin-Subdivision |
- 1.
- Erzeuge eine Liste pfl, die zu jedem Kontrollpunkt die
Polygone angibt, die diesen Punkt enthalten. Mit Hilfe von
pfl können im folgenden die zu den Punkten gehörenden
Polygone gefunden werden. Dazu bearbeite jedes Polygon
facet des G-Spline-Kontrollnetzes einzeln und unterscheide
für jeden Punkt eines solchen Polygons die beiden Fälle:
- (a)
- Wenn der Punkt noch nicht in der Liste vorhanden ist,
erzeuge ein neues Element in der Liste für diesen Punkt mit dem
Polygon facet.
- (b)
- Wenn der Punkt schon in der Liste vorhanden ist, füge das
Polygon facet dem entsprechenden Element hinzu.
- 2.
- Erzeuge eine Liste efl, die zu jeder Kante die
Polygone angibt, die diese Kante enthalten. Mit Hilfe von
efl können im folgenden die zu den Kanten gehörenden
Polygone gefunden werden. Dazu bearbeite jedes Polygon
facet des G-Spline-Kontrollnetzes einzeln und
unterscheide für jede Kante eines solchen Polygons die Fälle:
- (a)
- Wenn die Kante noch nicht in der Liste ist, erzeuge ein
neues Element für diese Kante und gebe facet als erstes
Polygon für diese Kante an.
- (b)
- Wenn schon ein Element für die Kante in der Liste
vorhanden ist und bis jetzt nur ein Polygon für diese Kante
aufgelistet wird, dann füge facet als zweites Polygon
hinzu.
- (c)
- Wenn schon ein Element für die Kante in der Liste
vorhanden ist und bereits zwei Polygone für diese Kante
aufgelistet werden, dann gib eine Warnung aus und ignoriere
facet für diese Kante. Eigentlich ist in diesem Fall ein
Fehler in dem Kontrollnetz vorhanden, da für eine Fläche eine
Kante maximal in zwei Polygonen vorhanden sein darf. Es genügt
aber dies einfach zu ignorieren und den Benutzer darüber zu
informieren.
- 3.
- Erzeuge für jeden Kontrollpunkt P und jedes über
pfl bestimmte Polygon facet, das diesen Punkt
enthält, einen neuen Kontrollpunkt Q als Mittel der
Kantenpunkte, des Gitterpunktes und P:
- (a)
- Bestimme den Punkt n nach P
und den Punkt p vor P in facet.
- (b)
- Bestimme die Kantenpunkte als Mittel von n und
P bzw. von p und P.
- (c)
- Bestimme den Gitterpunkt als Mittel aller Punkte
von facet.
- (d)
- Der neue Kontrollpunkt Q ist das Mittel der beiden
Kantenpunkte, des Gitterpunktes und P. Speichere
Q als neuen Kontrollpunkt für P und
facet.
- 4.
- Verbinde für jedes Polygon poly die neuen, für dieses
Polygon erzeugten Punkte:
- (a)
- Erzeuge ein neues Polygon-Objekt npoly.
- (b)
- Die für poly erzeugten neuen Kontrollpunkte bilden die
Punkte von npoly.
- (c)
- Füge npoly dem neuen Kontrollnetz hinzu.
- 5.
- Verbinde für jeden Kontrollpunkt P die für diesen Punkt
erzeugten, neuen Kontrollpunkte:
- (a)
- Erzeuge ein neues Polygon-Objekt npoly.
- (b)
- Die für P erzeugten, neuen Kontrollpunkte bilden die
Punkte von npoly. Die neuen Punkte müssen
entsprechend der Anordnung der zugehörigen Polygone miteinander
verbunden werden.
- (c)
- Falls das soeben erzeugte Polygon nicht geschlossen ist, also
an einem Rand des alten Kontrollnetzes liegt, dann lösche
npoly. Sonst füge npoly dem neuen Kontrollnetz
hinzu.
- 6.
- Verbinde für jede Kante E die neuen Punkte, die zu den
angrenzenden Polygonen gehören:
- (a)
- Erzeuge ein neues Polygon-Objekt npoly.
- (b)
- Finde die beiden Polygone, die die Kante E enthalten.
- (c)
- Die neuen Kontrollpunkte, die für die beiden Polygone und die
Endpunkte der Kante E erzeugt wurden, bilden die Punkte
für npoly.
- (d)
- Füge npoly dem neuen Kontrollnetz hinzu.
- 7.
- Ersetze das alte Kontrollnetz durch das neue Kontrollnetz.
Zwei irreguläre, nebeneinander liegende Polygone des alten
Kontrollnetzes werden durch Ausführen dieses Algorithmus' durch ein
reguläres Polygon getrennt. Führt man den Algorithmus zweimal aus,
sind sicher alle Irregularitäten durch wenigstens zwei reguläre
Polygone getrennt und der G-Spline-Algorithmus kann auf das
Kontrollnetz angewendet werden.
In Abbildung 1.19 wird ein einfacher Würfel gezeigt, auf
den dann zweimal der Doo-Sabin-Algorithmus angewendet wurde. Das
Bild oben zeigt das ursprüngliche Kontrollnetz, unterhalb wird dann
das ursprüngliche Kontrollnetz mit dem ersten Doo-Sabin-Schritt und
das Kontrollnetz nach zwei Doo-Sabin-Schritten gezeigt. Unten in der
Mitte ist die hierdurch erzeugte G-Spline-Fläche dargestellt.
Weitere Beispiele hierzu sind die
Abbildungen 1.20, 1.21, 1.22, 1.23
und 1.24. Alle ursprünglichen Kontrollnetze dieser
Beispiele wurden durch Zusammensetzen von Würfeln erzeugt, von denen
einzelne um eine Achse verdreht wurden (siehe 4.3.1).
Neben dem Doo-Sabin-Subdivision-Algorithmus gibt es auch noch die
Catmull-Clark-Subdivision. Dieser Subdivision-Algorithmus
verallgemeinert die bikubische, uniforme B-Spline-Verfeinerung für
beliebige Topologien. Wir werden diesen Algorithmus allerdings nicht
implementieren. Für eine genaue Beschreibung sei auf [CC78]
verwiesen.
Abbildung 1.19:
Doo-Sabin: Einfacher Würfel
|
|
Abbildung 1.20:
Doo-Sabin: Verdrehter Würfel
|
|
Abbildung 1.21:
Doo-Sabin: Acht
|
|
Abbildung 1.22:
Doo-Sabin: Verdrehte Acht
|
|
Abbildung 1.23:
Doo-Sabin: Kreuz
|
|
Abbildung 1.24:
Doo-Sabin: T
|
|



Next: 2. Funktionen auf Flächen
Up: 1. Kurven und Flächen
Previous: 1.8 Algorithmen für biquadratische
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node15.html
