


Next: 1.9 Doo-Sabin-Subdivision
Up: 1. Kurven und Flächen
Previous: 1.7 Biquadratische G-Splines
Inhalt
Wir werden nun die Algorithmen zur Berechnung und Darstellung der
biquadratischen G-Spline-Flächen vorstellen. Dazu führen wir
zunächst eine Datenstruktur ein, mit der wir allgemein die
geometrischen Objekte für eine Szene beschreiben können. Wir
beschränken uns momentan darauf, nur die grobe Struktur anzugeben. Die
vollständige Dokumentation der Klassenstruktur in C++ ist im
Anhang A zur Programm-Dokumentation beschrieben.
Abbildung 1.13:
World Klasse
 |
Abbildung 1.14:
Object und davon abgeleitete Klassen
 |
Eine einzelne Szene fassen wir zu einer World Klasse
zusammen. Diese Klasse enthält zunächst die generellen Eigenschaften
der Szene, Informationen zur Projektionsmethode, zum Betrachter und
über das Fenster, in dem die Szene angezeigt werden soll. Weiter
enthält sie eine Liste von grafischen Objekten, die zu der Szene
gehören, eine Liste der Lichtquellen und schließlich eine Liste der
Objekte, die angezeigt werden sollen. Die Objekte in der letzten Liste
müssen auch in der Liste aller grafischen Objekte vorhanden sein. Es
können durchaus Objekte zur Szene gehören, die nicht angezeigt, aber
zu deren Aufbau benötigt werden. Dies können z.B. Teile eines
Kontrollnetzes sein. Die Klasse stellt auch Methoden zur Darstellung
und Bearbeitung der Objekte zur Verfügung. Dabei muß zunächst die
Methode zur Bearbeitung der Objekte aufgerufen werden, die z.B. die
G-Spline-Kontrollnetze in Bézierkontrollnetze umwandelt. Die
Methode zur Darstellung zeichnet die vorher bearbeiteten,
darzustellenden Objekte direkt. Abbildung 1.13
zeigt den groben Aufbau dieser Klasse.
Die grafischen Objekte können Punkte, Polygone, G-Splines, etc.
sein, aber auch Lichtquellen können so beschrieben werden. Die
Lichtquellen werden in der World Klasse aus Effizienzgründen
in einer speziellen Liste eingetragen. Die Klassen für diese Objekte
werden alle von der Klasse Object abgeleitet. Dabei enthält
Object die allgemeinen Eigenschaften eines solchen grafischen
Objekts. Dies sind z.B. ein Bezeichner für das Objekt, die
Materialeigenschaften und Methoden zum Darstellen, Bearbeiten, etc.
des Objekts. Für die speziellen Typen der Objekte kommen dann weitere
spezielle Eigenschaften hinzu. Teilweise werden auch spezielle
Methoden zum Darstellen und Bearbeiten des Objekts zur Verfügung
gestellt. Für ein Polygon speichern wir z.B. als zusätzliche
Eigenschaft eine Liste von Punkt-Objekten, die die Kanten des
Polygons beschreiben. Ein G-Spline-Objekt enthält dann eine Liste
von Polygon-Objekten, aus denen das G-Spline-Kontrollnetz aufgebaut
ist. Weiter enthält es eine Liste von Bézierkontrollnetzen für
biquadratische Bézierflächen, die aus dem Kontrollnetz erzeugt
wurden. Wir werden später weitere Eigenschaften und Objekte
hinzufügen. Die grobe Struktur der Object Klassen wird in
Abbildung 1.14 dargestellt.
Ein Kontrollnetz einer G-Spline-Fläche wird durch Punkte
dargestellt, die durch Polygone zu einem Netz verbunden sind. Soweit
die Fläche selbst orientierbar ist, sollte jedes dieser Polygone die
gleiche Orientierung besitzen. Für einen einfachen
G-Spline-Algorithmus benötigen wir die Orientierung allerdings
nicht. Sie wird aber für bestimmte Darstellungen von Funktionen auf
den Flächen notwendig. Auch können wir die Orientierung bei der
Berechnung des G-Splines ausnutzen. Wir setzen aber nicht voraus, daß
die Polygone gleich mit der richtigen Orientierung vorgegeben wurden.
Der Algorithmus gspline_orientation orientiert die Polygone
eines G-Spline-Kontrollnetzes.
Algorithmus 1.1
| gspline_orientation |
| G-Spline-Kontrollnetz orientieren |
- 1.
- Falls das Kontrollnetz der G-Spline-Fläche schon als orientiert
markiert ist, ist nichts zu tun.
- 2.
- Erzeuge eine Liste pfl, die zu jedem Kontrollpunkt
die Polygone angibt, die diesen Punkt enthalten. Dazu bearbeite
jedes Polygon facet des G-Spline-Kontrollnetzes einzeln:
- (a)
- Für jeden Punkt eines solchen Polygons unterscheide
die beiden Fälle:
- i.
- Wenn der Punkt noch nicht in der Liste pfl
vorhanden ist, füge ein neues Element für diesen Punkt mit dem
Polygon facet hinzu.
- ii.
- Wenn der Punkt schon in der Liste vorhanden ist, füge das
Polygon facet zu dem Element hinzu.
- 3.
- Markiere alle Polygone als nicht orientiert.
- 4.
- Orientiere jedes Polygon allpolygon des
G-Spline-Kontrollnetzes. Dazu führe Folgendes für jedes
allpolygon aus:
- (a)
- Falls das Polygon allpolygon nicht orientiert ist,
verwende die Orientierung des Polygons allpolygon um alle
Polygone zu orientieren, die in dem zusammenhängenden Teilnetz
von allpolygon liegen:
- i.
- Markiere allpolygon als orientiert.
- ii.
- Falls vom Benutzer gefordert wird die Orientierung der
Fläche zu ändern, drehe die Reihenfolge der Punkte in
allpolygon um.
- iii.
- Füge allpolygon in die leere Polygonliste
poly_list ein.
- iv.
- Nun orientiere alle Polygone, die
zum zusammenhängenden Teilnetz von allpolygon
gehören. Dazu wiederhole Folgendes, solange
poly_list nicht leer ist:
- a.
- Entferne das erste Element polygon aus
poly_list.
- b.
- Finde für jede Kante von polygon die anderen
Polygone, die diese Kante enthalten. Benutze dazu die am
Anfang erzeugte Liste pfl.
- c.
- Jedes dieser anderen Polygone polygon2 muß die
entsprechende Kante in die entgegengesetzte Richtung
durchlaufen, damit die Orientierung korrekt ist.
Unterscheide hierfür folgende Fälle:
- a.
- Wenn die Kante in polygon2
entgegengesetzt durchlaufen wird und polygon2
noch nicht als orientiert markiert ist, dann markiere es
als orientiert und füge es zur Liste poly_list
hinzu.
- b.
- Wenn die Kante in polygon2
entgegengesetzt durchlaufen wird und polygon2 als
orientiert markiert ist, ignoriere es.
- c.
- Wenn die Kante in polygon2 in der
gleichen Richtung durchlaufen wird und polygon2
als nicht orientiert markiert ist, dann drehe die
Reihenfolge der Punkte in polygon2 um, markiere
es als orientiert und füge es zur Liste
poly_list hinzu.
- d.
- Wenn die Kante in polygon2 in der
gleichen Richtung durchlaufen wird und polygon2
als orientiert markiert ist, dann ist die Fläche nicht
orientierbar. Gib eine entsprechende Warnung aus.
Damit obiger Algorithmus funktioniert, muß die Fläche orientierbar
sein. Bei nicht orientierbaren Flächen wird lediglich die Anzahl der
Kanten, an denen das Kontrollnetz nicht orientiert ist, reduziert. Es
bleiben die Kanten übrig, für die der Fall d. von IV-A-4
zutrifft. Dies kann an beliebigen Stellen im Kontrollnetz erfolgen,
ohne daß diese Kanten miteinander verbunden sind und hängt von der
Reihenfolge ab, in der die Polygone bearbeitet werden.
Normalerweise nehmen wir auch an, daß nur maximal zwei Polygone eine
gemeinsame Kante haben. Der Algorithmus funktioniert aber auch, wenn
es mehr Polygone sind, allerdings kann man dann genau genommen nicht
mehr von einer Orientierung sprechen. Spätestens bei der Umwandlung
des Kontrollnetzes in Bézierpunkte werden an solchen Stellen nur
noch zwei Polygone berücksichtigt. Welche dies sind, ist dabei nicht
festgelegt und hängt wieder von der Reihenfolge ab, in der die
Polygone bearbeitet werden.
Es bietet sich auch an, die Liste pfl durch eine weiteres
Objekt zu repräsentieren, da wir solche und ähnliche Listen häufiger
benötigen. Wir werden sie also durch eine Klasse implementieren, die
Methoden zur Umwandlung des Kontrollnetzes in eine solche Liste
enthält.
Unser nächstes Ziel ist die Entwicklung eines Algorithmus, der die
Kontrollpunkte für die G-Spline-Fläche in Bézierpunkte für
biquadratische Bézierflächen nach Theorem 1.8
umwandelt. Hier ist das Hauptproblem, die entsprechenden Punkte in dem
über Polygone definierten semi-regulären Kontrollnetz zu finden. Dazu
behandeln wir zunächst alle irregulären Stellen des Netzes. Jedes
Polygon 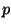 des Kontrollnetzes mit mehr oder weniger als vier Punkten
beschreibt eine Irregularität. Die Punkte in der Umgebung dieses
Polygons werden unter Berücksichtigung der Orientierung durch
folgenden Algorithmus bestimmt und über Theorem 1.8
werden die Bézierpunkte berechnet. Dabei werden zunächst nur die
Flächenstücke für die Punkte des Polygons
des Kontrollnetzes mit mehr oder weniger als vier Punkten
beschreibt eine Irregularität. Die Punkte in der Umgebung dieses
Polygons werden unter Berücksichtigung der Orientierung durch
folgenden Algorithmus bestimmt und über Theorem 1.8
werden die Bézierpunkte berechnet. Dabei werden zunächst nur die
Flächenstücke für die Punkte des Polygons 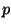 berechnet und die
Quasikontrollpunkte gespeichert. Denn die Gleichungen für den äußeren
Ring um
berechnet und die
Quasikontrollpunkte gespeichert. Denn die Gleichungen für den äußeren
Ring um 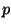 stimmen mit dem regulären Fall überein, falls die
Quasikontrollpunkte verwendet werden. Nachdem alle Irregularitäten
behandelt wurden, werden die restlichen Bézierpunkte für den
regulären Fall berechnet, wobei die entsprechenden Quasikontrollpunkte
und die schon berechneten Bézierpunkte berücksichtigt werden.
stimmen mit dem regulären Fall überein, falls die
Quasikontrollpunkte verwendet werden. Nachdem alle Irregularitäten
behandelt wurden, werden die restlichen Bézierpunkte für den
regulären Fall berechnet, wobei die entsprechenden Quasikontrollpunkte
und die schon berechneten Bézierpunkte berücksichtigt werden.
Abbildung 1.15:
G-Spline-Kontrollpunkte im irregulären Fall
|
|
Algorithmus 1.2
| process_gspline_object |
| G-Spline-Kontrollnetz in Bézierkontrollnetze umwandeln |
- 1.
- Orientiere das G-Spline-Kontrollnetz mit gspline_orientation.
- 2.
- Erzeuge eine Liste pfl, die zu jedem Kontrollpunkt die
Ordnung und die Polygone angibt, die diesen Punkt enthalten.
Bearbeite dazu jedes Polygon facet des
G-Spline-Kontrollnetzes einzeln:
- (a)
- Bestimme zunächst die Anzahl n der Punkte des Polygons.
- (b)
- Für jeden Punkt des Polygons unterscheide die beiden Fälle:
- i.
- Wenn der Punkt schon in der Liste vorhanden ist, füge
das Polygon facet zu dem Element hinzu:
- a.
- Falls n nicht 4 ist, setze die Ordnung des
Punktes in der Liste auf n. Sollte die Ordnung des
Punktes in der Liste vorher schon von 4 verschieden sein,
dann liegen zwei irreguläre Teile des Netzes nebeneinander.
Beende in diesem Fall den Algorithmus mit einer entsprechenden
Fehlermeldung.
- b.
- Falls das Element für den Punkt in pfl wenigstens 4
Polygone auflistet, die diesen Punkt enthalten, dann
beende den Algorithmus ebenfalls mit einer entsprechenden
Fehlermeldung.
- c.
- Füge facet dem Element für den Punkt in
pfl hinzu.
- ii.
- Wenn der Punkt noch nicht in der Liste vorhanden ist,
erzeuge ein neues Element in der Liste für diesen Punkt mit dem
Polygon facet und der Ordnung n.
- 3.
- Berechne die Bézierkontrollnetze für die irregulären Teile
des G-Spline-Kontrollnetzes. Betrachte dazu jeden Punkt p
aus der Liste pfl mit der Ordnung n ungleich 4
der in 4 Polygone des Kontrollnetzes enthalten ist und noch nicht
bearbeitet wurde. Die Bézierkontrollnetze für diese Irregularität
werden wie folgt erzeugt:
- (a)
- Finde das Polygon fi, das genau n Punkte
enthält, von denen einer p ist. Dies ist das Polygon
welches die Irregularität im Netz erzeugt.
- (b)
- Bestimme die Punkte D (vgl. Abbildung 1.15)
als Punkte von fi. Die
Numerierung sei durch die Reihenfolge der Punkte in fi
beginnend mit p festgelegt.
- (c)
- Markiere alle Punkte D als bearbeitet.
- (d)
- Wenn einer der Punkte D nicht genau in 4 Polygonen
enthalten ist, fahre mit dem nächsten Punkt fort, da die
Irregularität nicht vollständig ist.
- (e)
- Finde das Polygon D[0], J[0], L[0],
F[0] (vgl. Abbildung 1.15). Dies
ist das einzige Polygon, das D[0] enthält, aber nicht
D[1] und D[n-1]. Nehme zunächst an, daß die
Punkte J[0], L[0], F[0] dem Punkt
D[0] in dieser Reihenfolge im Polygon folgen.
- (f)
- Finde den Punkt J[1]. Suche dazu das Polygon, welches
D[1], D[0] und F[0] in dieser
Reihenfolge enthält. Existiert dieses Polygon nicht, dann stimmt
die vorher gewählte Orientierung an dieser Stelle nicht. Suche in
diesem Fall das Polygon mit der Kante von D[1] nach
D[0] und vertausche J[0] und F[0]. In
beiden Fällen ist J[1] der fehlende Punkt des Polygons.
- (g)
- Bestimme die restlichen Punkte F[k], L[k],
J[k+1] für
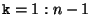 (vgl. Abbildung 1.15):
(vgl. Abbildung 1.15):
- i.
- Finde das Polygon D[k], J[k],
L[k], F[k]. Dazu suche zunächst das Polygon,
das die Kante D[k], J[k] enthält. Folgt diesen
Punkten im Polygon nicht F[k-1], dann sind die nächsten
beiden Punkte des Polygons L[k] und F[k]. Wird
dieses Polygon nicht gefunden, dann stimmt die Orientierung an
dieser Stelle nicht. Suche in diesem Fall das Polygon mit der
Kante von J[k] nach D[k]. Folgt auf diese
Kante im Polygon nicht D[k-1], dann sind die nächsten
beiden Punkte des Polygon F[k] und L[k].
- ii.
- Ist k kleiner als
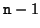 , dann bestimme
J[k+1]. Dazu suche zunächst das Polygon mit der Kante
von D[k] nach F[k]. Ist der nächste Punkt in
diesem Polygon nicht der Punkt D[k+1], dann ist dieser
J[k+1]. Existiert ein solches Polygon nicht, dann
stimmt die Orientierung an dieser Stelle nicht. In diesem Fall suche
das Polygon mit der Kante von D[k] nach D[k+1].
Folgt hier nicht der Punkt F[k], dann ist dies der Punkt
J[k+1].
, dann bestimme
J[k+1]. Dazu suche zunächst das Polygon mit der Kante
von D[k] nach F[k]. Ist der nächste Punkt in
diesem Polygon nicht der Punkt D[k+1], dann ist dieser
J[k+1]. Existiert ein solches Polygon nicht, dann
stimmt die Orientierung an dieser Stelle nicht. In diesem Fall suche
das Polygon mit der Kante von D[k] nach D[k+1].
Folgt hier nicht der Punkt F[k], dann ist dies der Punkt
J[k+1].
- (h)
- Berechne die Quasikontrollpunkte
Dv, Fv, Jv, Lv aus
D, F, J, L
über (1.48).
- (i)
- Berechne die Bézierpunkte A, B,
C, E, G, H, I,
K, M aus den Quasikontrollpunkten über die
Gleichungen (1.45).
- (j)
- Erzeuge für jeden Kontrollpunkt das entsprechende
Bézierkontrollnetz aus den bisher berechneten Punkten und füge
es zur Liste der Bézierkontrollnetze des G-Splines mit einer
Referenz auf den Kontrollpunkt hinzu.
- (k)
- Speichere für jeden Kontrollpunkt D, F,
J, L zusätzlich die Position des zugehörigen
Quasikontrollpunktes. Diese wird dazu verwendet den äußeren Ring
der Bézierpunkte im nächsten Teil des Algorithmus' zu berechnen.
- 4.
- Berechne die Bézierkontrollnetze für die regulären (noch
nicht bearbeiteten) Teile des G-Spline-Kontrollnetzes. Hierzu wird
ein Bézierkontrollnetz für jeden Punkt m aus der Liste
pfl der Ordnung 4 erzeugt, der in 4 Polygonen des
G-Spline-Kontrollnetzes enthalten ist und noch nicht bearbeitet
wurde (vgl. Abbildung 1.17):
- (a)
- Wähle ein beliebiges Polygon f0 aus, das m
enthält und markiere dieses Polygon als benutzt.
- (b)
- Wähle Punkte n0, nn0, n1 als die
Punkte, die m in der Punktliste des Polygons in dieser
Reihenfolge folgen.
- (c)
- Finde das Polygon f1. Dazu suche in allen nicht als
benutzt markierten Polygonen, die m enthalten, die Kante
von m nach n1. Nach diesen beiden Punkten folgen
die Punkte nn1 und n2. Wird die Kante in die
entgegengesetzte Richtung durchlaufen, stimmt die Orientierung an
dieser Stelle nicht. In diesem Fall folgen auf die Kante von
n1 nach m die Punkte n2, nn1.
Markiere schließlich das Polygon f1 als benutzt.
- (d)
- Finde das Polygon f2 analog zu f1, wobei die
gesuchte Kante nun m, n2 ist. nn2,
n3 folgen entsprechend der Orientierung.
- (e)
- Finde nn3 in dem noch nicht als benutzt markierten
Polygon, das m enthält. Unabhängig von der Orientierung
ist nn3 in diesem Polygon der zweite Punkt nach
m.
- (f)
- Erzeuge das Bézierkontrollnetz für m
nach (1.38) für den regulären Fall. Dazu werden
im wesentlichen die Mittel der für die Bézierpunkte zuständigen
Kontrollpunkte berechnet. Falls allerdings Quasikontrollpunkte für
die Kontrollpunkte im irregulären Fall berechnet wurden oder schon
Bézierkontrollnetze für die angrenzenden Flächenstücke
existieren, verwende die Koordinaten dieser Punkte. Sollten für
die vorher bestimmten Punkte schon Bézierkontrollnetze berechnet
worden sein, dann verwende die Koordinaten des mittleren
Bézierpunktes. Falls ein Quasikontrollpunkt für diese Punkte
berechnet wurde, verwende die Koordinaten des
Quasikontrollpunktes. Sonst verwende die Koordinaten des
Kontrollpunktes.
Abbildung 1.16:
Möbiusband
|
|
In Schritt III-H wird zur Berechnung der
Quasikontrollpunkte die Matrix 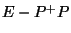 für die
Gleichung (1.48) benötigt. Da diese Matrix nur von der
Ordnung der Irregularität abhängt, genügt es aber, sie pro benötigter
Ordnung nur einmal zu berechnen und sie für weitere Berechnungen zu
speichern.
für die
Gleichung (1.48) benötigt. Da diese Matrix nur von der
Ordnung der Irregularität abhängt, genügt es aber, sie pro benötigter
Ordnung nur einmal zu berechnen und sie für weitere Berechnungen zu
speichern.
Abbildung 1.17:
G-Spline-Kontrollpunkte im regulären Fall
 |
Wurde die G-Spline-Fläche in biquadratische Bézierkontrollnetze
umgewandelt, läßt sich die Fläche durch Standardalgorithmen für
Bézierflächen darstellen. Auf den genauen Algorithmus zur
Visualisierung gehen wir deshalb hier nicht näher ein.
Abbildung 1.16 zeigt ein Möbiusband, das durch ein
reguläres Kontrollnetz beschrieben wird. Dieses Netz wurde allerdings
schon mit dem im nächsten Abschnitt beschriebenen
Doo-Sabin-Subdivision-Algorithmus aus einem vereinfachten
Kontrollnetz erzeugt.



Next: 1.9 Doo-Sabin-Subdivision
Up: 1. Kurven und Flächen
Previous: 1.7 Biquadratische G-Splines
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node14.html

![]() des Kontrollnetzes mit mehr oder weniger als vier Punkten
beschreibt eine Irregularität. Die Punkte in der Umgebung dieses
Polygons werden unter Berücksichtigung der Orientierung durch
folgenden Algorithmus bestimmt und über Theorem 1.8
werden die Bézierpunkte berechnet. Dabei werden zunächst nur die
Flächenstücke für die Punkte des Polygons
des Kontrollnetzes mit mehr oder weniger als vier Punkten
beschreibt eine Irregularität. Die Punkte in der Umgebung dieses
Polygons werden unter Berücksichtigung der Orientierung durch
folgenden Algorithmus bestimmt und über Theorem 1.8
werden die Bézierpunkte berechnet. Dabei werden zunächst nur die
Flächenstücke für die Punkte des Polygons ![]() berechnet und die
Quasikontrollpunkte gespeichert. Denn die Gleichungen für den äußeren
Ring um
berechnet und die
Quasikontrollpunkte gespeichert. Denn die Gleichungen für den äußeren
Ring um ![]() stimmen mit dem regulären Fall überein, falls die
Quasikontrollpunkte verwendet werden. Nachdem alle Irregularitäten
behandelt wurden, werden die restlichen Bézierpunkte für den
regulären Fall berechnet, wobei die entsprechenden Quasikontrollpunkte
und die schon berechneten Bézierpunkte berücksichtigt werden.
stimmen mit dem regulären Fall überein, falls die
Quasikontrollpunkte verwendet werden. Nachdem alle Irregularitäten
behandelt wurden, werden die restlichen Bézierpunkte für den
regulären Fall berechnet, wobei die entsprechenden Quasikontrollpunkte
und die schon berechneten Bézierpunkte berücksichtigt werden.
![]() für die
Gleichung (1.48) benötigt. Da diese Matrix nur von der
Ordnung der Irregularität abhängt, genügt es aber, sie pro benötigter
Ordnung nur einmal zu berechnen und sie für weitere Berechnungen zu
speichern.
für die
Gleichung (1.48) benötigt. Da diese Matrix nur von der
Ordnung der Irregularität abhängt, genügt es aber, sie pro benötigter
Ordnung nur einmal zu berechnen und sie für weitere Berechnungen zu
speichern.