


Next: 2.2 Darstellung von Funktionen
Up: 2. Funktionen auf Flächen
Previous: 2. Funktionen auf Flächen
Inhalt
Wie in Abschnitt 1.6 wollen wir zunächst zwei
Bézierflächen 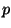 und
und 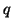 geometrisch glatt zusammensetzen. Die
beiden Flächenstücke seien als Bézierflächenstücke mit den
Kontrollpunkten
geometrisch glatt zusammensetzen. Die
beiden Flächenstücke seien als Bézierflächenstücke mit den
Kontrollpunkten 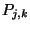 und
und 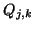 gegeben,
gegeben,
Wir nehmen an, daß 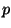 und
und 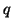 eine gemeinsame Randkurve
eine gemeinsame Randkurve
![c: [0,1] -> R^3](img169.png) besitzen. Diese sei o.B.d.A. gegeben durch
besitzen. Diese sei o.B.d.A. gegeben durch
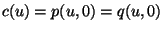 für für ![u \in [0,1].](img314.png) |
(2.3) |
Weiter seien auf den beiden Bézierflächen
![P := p([0,1]^2)](img315.png) und
und
![Q := q([0,1]^2)](img316.png) zwei stetige differenzierbare
Abbildungen
zwei stetige differenzierbare
Abbildungen
gegeben mit
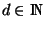 . Wir folgen nun dem Ansatz aus [Sey96], um
diese beiden Funktionen stetig differenzierbar zusammenzusetzen.
Abbildung 2.1 zeigt eine schematische Darstellung
dieser Situation.
. Wir folgen nun dem Ansatz aus [Sey96], um
diese beiden Funktionen stetig differenzierbar zusammenzusetzen.
Abbildung 2.1 zeigt eine schematische Darstellung
dieser Situation.
Wenn (1.34) für 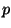 und
und 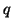 erfüllt ist, erhalten wir eine
längs
erfüllt ist, erhalten wir eine
längs 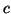 geometrisch glatt zusammengesetzte Fläche
geometrisch glatt zusammengesetzte Fläche
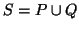 . Unter
bestimmten Bedingungen an
. Unter
bestimmten Bedingungen an 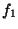 und
und 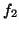 erzeugen diese beiden
Funktionen eine stetig differenzierbare Funktion
erzeugen diese beiden
Funktionen eine stetig differenzierbare Funktion
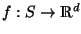 mit
mit
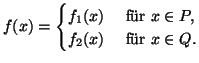 |
(2.6) |
Da 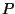 und
und  die gemeinsame Randkurve
die gemeinsame Randkurve  besitzen, muß
besitzen, muß
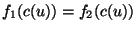 für für ![u \in [0,1]](img328.png) |
(2.7) |
gelten, damit 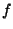 wohldefiniert ist. Aus der Stetigkeit von
wohldefiniert ist. Aus der Stetigkeit von 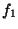 und
und
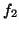 und aus (2.7) folgt, daß
und aus (2.7) folgt, daß 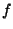 längs
längs 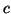 stetig
ist.
stetig
ist.
Abbildung 2.1:
Zusammensetzen von Funktionen auf Flächenstücken
|
|
Wir suchen nun noch eine Bedingung für die Differenzierbarkeit von 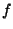 längs
längs 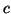 . Dazu benötigen wir eine Parametrisierung
. Dazu benötigen wir eine Parametrisierung 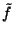 von
von
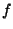 , die differenzierbar ist. Zunächst werden wir eine stetig
differenzierbare Parametrisierung
, die differenzierbar ist. Zunächst werden wir eine stetig
differenzierbare Parametrisierung
![s: [0,1]^2 -> R^3](img340.png) für
für 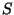 angeben. Diese erhalten wir durch das Kombinieren von
angeben. Diese erhalten wir durch das Kombinieren von 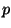 und
und 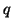 . Wir
wählen dazu zwei stetig differenzierbare Transformationen
. Wir
wählen dazu zwei stetig differenzierbare Transformationen
![t_i: [0,1]^2 -> A_i \subset [0,1]^2, i = 1, 2](img341.png) |
(2.8) |
mit
![A_1 \intersection A_2 = t_1([0,1],0) = t_2([0,1],0)](img342.png) . Die Parametrisierung
sei dann über
. Die Parametrisierung
sei dann über
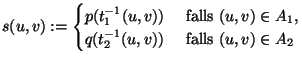 |
(2.9) |
gegeben. Nach (2.3) ist dies wohldefiniert.
Um die Transformationen explizit zu bestimmen, wählen wir
![t_1(u,v) = [u, (1+v)/2]^T](img344.png) . Daraus
folgt
. Daraus
folgt
![t_2(u,0) = t_1(u,0) = [u; 1/2].](img345.png) |
(2.10) |
Aus der stetigen Differenzierbarkeit von  folgt
folgt
Aus (2.10) folgt
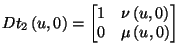 |
(2.14) |
mit den Funktionen 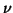 und
und 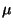 für die partiellen Ableitungen von
für die partiellen Ableitungen von
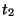 nach
nach 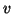 . Damit gilt
. Damit gilt
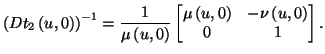 |
(2.15) |
Dies in (2.13) eingesetzt ergibt
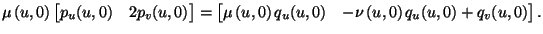 |
(2.16) |
Hieraus erhalten wir die Gleichungen
Aus (2.3) folgt sofort, daß (2.17) erfüllt
ist. Es bleibt also zunächst die Gleichung (2.18). Setzt
man (1.34) ein, ergibt dies
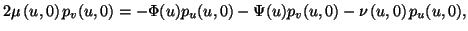 |
(2.19) |
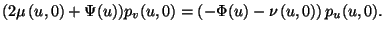 |
(2.20) |
Hieraus erhält man die Bedingungen
Dies bedeutet, daß
![Dt_2(u,0) = [1, -Phi(u); 0, -1/2Psi(u)].](img366.png) |
(2.23) |
Diese Bedingung wird z.B. erfüllt von
![t_2(u,v) = [u - v Phi(u); -v/2Psi(u)].](img367.png) |
(2.24) |
Nun können wir eine Bedingung für die Differenzierbarkeit von 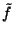 herleiten. Dazu seien
herleiten. Dazu seien
![~f_i: [0,1]^2 -> R^d](img368.png) für
für
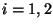 mit
mit
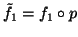 und
und
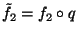 definiert. Es sei weiter
definiert. Es sei weiter
![~f: [0,1]^2 -> R^d](img372.png) gegeben durch
gegeben durch
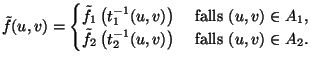 |
(2.25) |
Aus der Stetigkeit von 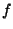 folgt
folgt
für
![u \in [0,1]](img376.png) . Weiter soll
. Weiter soll 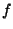 stetig differenzierbar sein,
d.h. es muß gelten
stetig differenzierbar sein,
d.h. es muß gelten
Mit (2.23) folgt
Dies liefert die Gleichungen
(2.33) ist wegen (2.27) erfüllt und
aus (2.34) erhält man deshalb
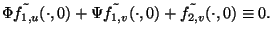 |
(2.35) |
Diese Bedingung stimmt formal mit der Bedingung (1.34) für
die geometrische Glattheit von Flächen überein. Dabei ist zu beachten,
daß 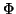 und
und 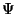 dieselben Funktionen sind, die beim
Zusammensetzen der Flächenstücke verwendet werden.
dieselben Funktionen sind, die beim
Zusammensetzen der Flächenstücke verwendet werden.



Next: 2.2 Darstellung von Funktionen
Up: 2. Funktionen auf Flächen
Previous: 2. Funktionen auf Flächen
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node17.html
![]() und
und ![]() geometrisch glatt zusammensetzen. Die
beiden Flächenstücke seien als Bézierflächenstücke mit den
Kontrollpunkten
geometrisch glatt zusammensetzen. Die
beiden Flächenstücke seien als Bézierflächenstücke mit den
Kontrollpunkten ![]() und
und ![]() gegeben,
gegeben,
![]() und
und ![]() erfüllt ist, erhalten wir eine
längs
erfüllt ist, erhalten wir eine
längs ![]() geometrisch glatt zusammengesetzte Fläche
geometrisch glatt zusammengesetzte Fläche
![]() . Unter
bestimmten Bedingungen an
. Unter
bestimmten Bedingungen an ![]() und
und ![]() erzeugen diese beiden
Funktionen eine stetig differenzierbare Funktion
erzeugen diese beiden
Funktionen eine stetig differenzierbare Funktion
![]() mit
mit
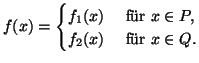
![]() längs
längs ![]() . Dazu benötigen wir eine Parametrisierung
. Dazu benötigen wir eine Parametrisierung ![]() von
von
![]() , die differenzierbar ist. Zunächst werden wir eine stetig
differenzierbare Parametrisierung
, die differenzierbar ist. Zunächst werden wir eine stetig
differenzierbare Parametrisierung
![]() für
für ![]() angeben. Diese erhalten wir durch das Kombinieren von
angeben. Diese erhalten wir durch das Kombinieren von ![]() und
und ![]() . Wir
wählen dazu zwei stetig differenzierbare Transformationen
. Wir
wählen dazu zwei stetig differenzierbare Transformationen
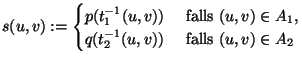
![]() . Daraus
folgt
. Daraus
folgt
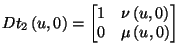
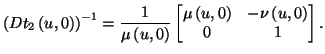
![t_2(u,v) = [u - v Phi(u); -v/2Psi(u)].](img367.png)
![]() herleiten. Dazu seien
herleiten. Dazu seien
![]() für
für
![]() mit
mit
![]() und
und
![]() definiert. Es sei weiter
definiert. Es sei weiter
![]() gegeben durch
gegeben durch
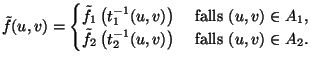
![]() und
und ![]() dieselben Funktionen sind, die beim
Zusammensetzen der Flächenstücke verwendet werden.
dieselben Funktionen sind, die beim
Zusammensetzen der Flächenstücke verwendet werden.