

Next: 1.7 Biquadratische G-Splines
Up: 1. Kurven und Flächen
Previous: 1.5 Tensorproduktflächen
Inhalt
1.6 Geometrisch glatte Flächen
Die Tensorproduktflächen der Form (1.29) lassen sich nun
ähnlich wie die Splinekurven geometrisch glatt zusammensetzen. Wir betrachten
die gesamte Fläche als aus Flächenstücken der Form (1.29) erzeugt,
wobei die Kontrollpunkte 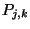 bestimmte Glattheitsbedingungen
erfüllen müssen. Dazu folgen wir hier dem Ansatz aus [Rei95].
bestimmte Glattheitsbedingungen
erfüllen müssen. Dazu folgen wir hier dem Ansatz aus [Rei95].
Seien die folgenden beiden Flächenstücke 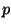 und
und 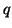 gegeben:
gegeben:
Beide werden vollständig durch die Kontrollpunkte 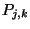 und
und 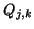 bestimmt. Zunächst fordern wir, daß
bestimmt. Zunächst fordern wir, daß 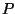 und
und 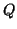 eine
gemeinsame Randkurve
eine
gemeinsame Randkurve
![c: [0,1] -> R^3](img169.png) besitzen. Dies werden wir im
folgenden auch als
besitzen. Dies werden wir im
folgenden auch als
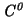 -Bedingung bezeichnen.
Durch die Forderung, daß die resultierende Fläche parametrisch glatt
sein soll, würden wir unsere Möglichkeiten erheblich einschränken.
Ähnlich wie bei den Kurven genügt es jedoch zu fordern, daß die Fläche
“nur” geometrisch glatt ist.
-Bedingung bezeichnen.
Durch die Forderung, daß die resultierende Fläche parametrisch glatt
sein soll, würden wir unsere Möglichkeiten erheblich einschränken.
Ähnlich wie bei den Kurven genügt es jedoch zu fordern, daß die Fläche
“nur” geometrisch glatt ist.
Definition 1.6 (Geometrische Glattheit)
Es seien zwei Flächenstücke durch die regulären Parametrisierungen
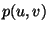
und
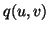
(
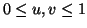
) mit einer gemeinsamen
Randkurve
![c: [0,1] -> R^3, c(u) = p(u,0) = q(u,0)](img173.png) für für ![t \in [0,1]](img174.png) |
(1.33) |
gegeben. Die aus den Flächenstücken zusammengesetzte Fläche ist
geometrisch glatt oder einmal stetig differenzierbar längs
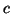
, wenn gilt
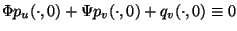 |
(1.34) |
mit
![Phi: [0,1] -> R](img176.png)
und
![Psi: [0,1] -> R^+](img177.png)
.
Dabei können natürlich beliebige Randkurven der beiden Flächenstücke
verwendet werden. Betrachten wir (1.34) genauer, dann
bedeutet dies zunächst, daß die Tangentialebenen von 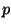 und
und 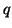 in
jedem Punkt von
in
jedem Punkt von 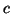 übereinstimmen. Die Tangentenebene in
übereinstimmen. Die Tangentenebene in 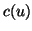 wird
von den beiden Vektoren
wird
von den beiden Vektoren
![[p_u(u,0), p_v(u,0)]](img179.png) bzw.
bzw.
![[q_u(u,0), q_v(u,0)]](img180.png) aufgespannt. Wegen (1.33) gilt
aufgespannt. Wegen (1.33) gilt
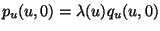 . Hieraus folgt dann die
Bedingung (1.34).
. Hieraus folgt dann die
Bedingung (1.34).
Offensichtlich genügt es jedoch nicht zu fordern, daß die
Tangentialebenen übereinstimmen. Man könnte so z.B. die gleiche Fläche
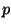 oder Flächen die sich längs
oder Flächen die sich längs 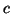 tangential wie
tangential wie 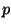 verhalten
zusammensetzen und so eine “Spitze” erhalten. Wir benötigen eine
weitere Bedingung, die sicherstellt, daß die beiden Flächen auf
“verschiedenen Seiten von
verhalten
zusammensetzen und so eine “Spitze” erhalten. Wir benötigen eine
weitere Bedingung, die sicherstellt, daß die beiden Flächen auf
“verschiedenen Seiten von 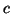 ” liegen. Betrachten wir die
Tangentialebene im Punkt
” liegen. Betrachten wir die
Tangentialebene im Punkt 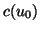 , dann wird sie durch die durch
, dann wird sie durch die durch
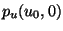 , bzw.
, bzw.
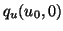 erzeugte Gerade in zwei Teilebenen
zerlegt. Wenn wir nun fordern, daß
erzeugte Gerade in zwei Teilebenen
zerlegt. Wenn wir nun fordern, daß
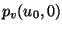 und
und
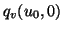 auf
verschiedenen Seiten dieser Geraden liegen, ergeben sich keine
“Spitzen” mehr. Um dies sicherzustellen genügt es wie in obiger
Definition zu fordern, daß
auf
verschiedenen Seiten dieser Geraden liegen, ergeben sich keine
“Spitzen” mehr. Um dies sicherzustellen genügt es wie in obiger
Definition zu fordern, daß 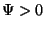 ist.
ist.
Die Gleichung (1.34) ist noch sehr allgemein. Wählt man
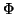 und
und 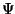 nach [Rei95], dann erhält man speziellere
Glattheitsbedingungen, die wir im folgenden für die G-Splines
verwenden werden.
nach [Rei95], dann erhält man speziellere
Glattheitsbedingungen, die wir im folgenden für die G-Splines
verwenden werden.
Wir werden nun alle drei Typen für biquadratische 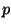 und
und 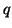 (d.h.
(d.h.
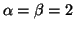 ) etwas näher untersuchen.
) etwas näher untersuchen.
Im Fall von Typ 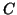 erhalten wir die Bedingung für die parametrische
Glattheit (
erhalten wir die Bedingung für die parametrische
Glattheit (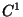 -Bedingung),
-Bedingung),
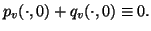 |
(1.35) |
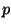 und
und 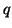 eingesetzt ergibt
eingesetzt ergibt
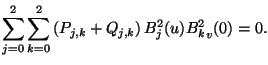 |
(1.36) |
Es gilt
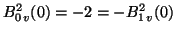 und
und
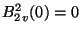 und
aus der
und
aus der 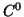 -Bedingung folgt, daß
-Bedingung folgt, daß
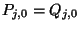 für
für 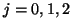 .
Also erhalten wir
.
Also erhalten wir
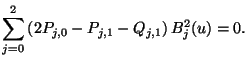 |
(1.37) |
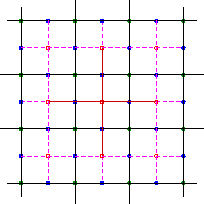
Abbildung 1.8:
Kontrollpunkte für Typ 
 |
Hieraus ergeben sich die folgenden Bedingungen für die Bézierpunkte:
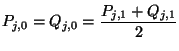 für für  |
(1.38) |
Bei einer Vierer-Nachbarschaftsstruktur, bei der die Flächenstücke an
allen vier Randkurven geometrisch glatt zusammengesetzt werden,
bestimmen damit die “mittleren” Bézierpunkte 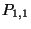 alle
anderen Bézierpunkte. Siehe hierzu auch
Abbildung 1.8. Hier können die
“mittleren”, mit nicht ausgefüllten Kreisen gekennzeichneten
Bézierpunkte, frei gewählt werden und die mit ausgefüllten Kreisen
markierten Bézierpunkte ergeben sich als Mittel der angrenzenden,
nicht ausgefüllten Bézierpunkte. Damit lassen sich alle regulären
Netze, die in diesem Fall die mittleren Bézierpunkte bestimmen, in
Bézierkontrollnetze umwandeln.
alle
anderen Bézierpunkte. Siehe hierzu auch
Abbildung 1.8. Hier können die
“mittleren”, mit nicht ausgefüllten Kreisen gekennzeichneten
Bézierpunkte, frei gewählt werden und die mit ausgefüllten Kreisen
markierten Bézierpunkte ergeben sich als Mittel der angrenzenden,
nicht ausgefüllten Bézierpunkte. Damit lassen sich alle regulären
Netze, die in diesem Fall die mittleren Bézierpunkte bestimmen, in
Bézierkontrollnetze umwandeln.
Für den 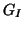 Typ erhalten wir die Gleichung
Typ erhalten wir die Gleichung
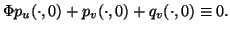 |
(1.39) |
Nachdem 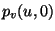 und
und  quadratisch in
quadratisch in 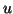 sind und
sind und
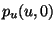 linear in
linear in 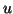 ist, ist die Funktion
ist, ist die Funktion 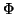 linear. Also sei
linear. Also sei
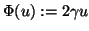 mit
mit
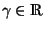 . Setzt man
dann (1.29) in (1.39) ein, erhält man folgende
Gleichungen für die Kontrollpunkte,
. Setzt man
dann (1.29) in (1.39) ein, erhält man folgende
Gleichungen für die Kontrollpunkte,
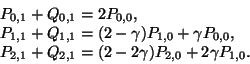 |
(1.40) |
Für Typ 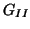 gilt die Gleichung
gilt die Gleichung
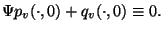 |
(1.41) |
Zur Lösung dieser Gleichung nehmen wir an, daß 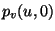 und
und
 im gleichen linearen Raum liegen, d.h.
im gleichen linearen Raum liegen, d.h.
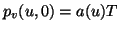 und
und
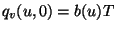 mit
mit
![a,b: [0,1] -> R](img220.png) und
und
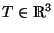 . Dann
ist die Gleichung für
. Dann
ist die Gleichung für
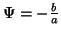 erfüllt. Eine sinnvolle
Bedingung für die Bézierpunkte ist somit
erfüllt. Eine sinnvolle
Bedingung für die Bézierpunkte ist somit
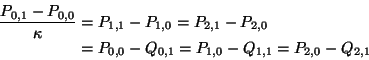 |
(1.42) |
mit
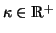 . Aus
. Aus
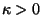 folgt daß
folgt daß
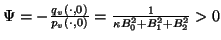 ,
wie ursprünglich gefordert.
,
wie ursprünglich gefordert.



Next: 1.7 Biquadratische G-Splines
Up: 1. Kurven und Flächen
Previous: 1.5 Tensorproduktflächen
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node12.html
![]() bestimmte Glattheitsbedingungen
erfüllen müssen. Dazu folgen wir hier dem Ansatz aus [Rei95].
bestimmte Glattheitsbedingungen
erfüllen müssen. Dazu folgen wir hier dem Ansatz aus [Rei95].
![]() und
und ![]() gegeben:
gegeben:
![]() und
und ![]() in
jedem Punkt von
in
jedem Punkt von ![]() übereinstimmen. Die Tangentenebene in
übereinstimmen. Die Tangentenebene in ![]() wird
von den beiden Vektoren
wird
von den beiden Vektoren
![]() bzw.
bzw.
![]() aufgespannt. Wegen (1.33) gilt
aufgespannt. Wegen (1.33) gilt
![]() . Hieraus folgt dann die
Bedingung (1.34).
. Hieraus folgt dann die
Bedingung (1.34).
![]() oder Flächen die sich längs
oder Flächen die sich längs ![]() tangential wie
tangential wie ![]() verhalten
zusammensetzen und so eine “Spitze” erhalten. Wir benötigen eine
weitere Bedingung, die sicherstellt, daß die beiden Flächen auf
“verschiedenen Seiten von
verhalten
zusammensetzen und so eine “Spitze” erhalten. Wir benötigen eine
weitere Bedingung, die sicherstellt, daß die beiden Flächen auf
“verschiedenen Seiten von ![]() ” liegen. Betrachten wir die
Tangentialebene im Punkt
” liegen. Betrachten wir die
Tangentialebene im Punkt ![]() , dann wird sie durch die durch
, dann wird sie durch die durch
![]() , bzw.
, bzw.
![]() erzeugte Gerade in zwei Teilebenen
zerlegt. Wenn wir nun fordern, daß
erzeugte Gerade in zwei Teilebenen
zerlegt. Wenn wir nun fordern, daß
![]() und
und
![]() auf
verschiedenen Seiten dieser Geraden liegen, ergeben sich keine
“Spitzen” mehr. Um dies sicherzustellen genügt es wie in obiger
Definition zu fordern, daß
auf
verschiedenen Seiten dieser Geraden liegen, ergeben sich keine
“Spitzen” mehr. Um dies sicherzustellen genügt es wie in obiger
Definition zu fordern, daß ![]() ist.
ist.
![]() und
und ![]() nach [Rei95], dann erhält man speziellere
Glattheitsbedingungen, die wir im folgenden für die G-Splines
verwenden werden.
nach [Rei95], dann erhält man speziellere
Glattheitsbedingungen, die wir im folgenden für die G-Splines
verwenden werden.
![]() und
und ![]() (d.h.
(d.h.
![]() ) etwas näher untersuchen.
) etwas näher untersuchen.
![]() erhalten wir die Bedingung für die parametrische
Glattheit (
erhalten wir die Bedingung für die parametrische
Glattheit (![]() -Bedingung),
-Bedingung),
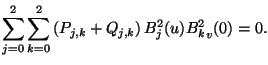
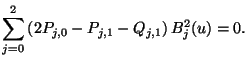
![]() Typ erhalten wir die Gleichung
Typ erhalten wir die Gleichung
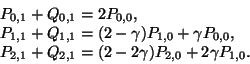
![]() gilt die Gleichung
gilt die Gleichung