Die formale Übereinstimmung von (2.35)
und (1.34) legt es nahe, Funktionen auf einer
Splinefläche wieder durch Splines darzustellen. Sei die biquadratische
Splinefläche ![]() durch (2.1) mit
durch (2.1) mit
![]() gegeben. Eine Funktion
gegeben. Eine Funktion
![]() auf dieser Fläche beschreiben
wir als biquadratischen Spline in der Form
auf dieser Fläche beschreiben
wir als biquadratischen Spline in der Form
Sei analog eine Funktion
![]() auf dem Flächenstück
auf dem Flächenstück ![]() durch
durch
![~f_2: [0,1]^2 -> R^d, ~f_2(u,v) = \sum_{j=0}^2 \sum_{k=0}^2 G_{j,k} B^2_j(u) B^2_k(v)](img403.png) |
(2.37) |
Ist die Fläche durch ein semi-reguläres Kontrollnetz gegeben, beschreiben wir eine Funktion auf dieser Fläche, indem wir zu jedem Kontrollpunkt der Fläche einen Kontrollpunkt für die Funktion angeben. Diese Form der Darstellung einer Funktion ist z.B. zur Darstellung von Meßwerten auf glatten Oberflächen geeignet.
Sowohl die Fläche als auch die Funktion werden dann durch
biquadratische G-Splines dargestellt. Neben der Umwandlung des
semi-regulären Kontrollnetzes in Bézierkontrollnetze durch den
Algorithmus 1.2 muß auch das
Kontrollnetz für die Funktion in Bézierkontrollnetze umgewandelt werden.
Nachdem ![]() und
und ![]() bereits durch die Fläche bestimmt werden,
können hierfür die gleichen Formeln wie für die Flächenkontrollpunkte
verwendet werden. Dazu müssen wir den
Algorithmus 1.2 erweitern. Zusätzlich
muß zu jedem Flächenkontrollpunkt der Funktionskontrollpunkt gefunden
werden und das Bézierkontrollnetz für die Funktion analog zu dem für die
Fläche berechnet werden. Ein Funktionsobjekt stellen wir dabei durch
eine von Object abgeleitete Klasse Function dar. Sie
enthält einen Zeiger auf die zugehörige G-Spline-Fläche und auf die
Map Klasse. Die Map Klasse ist eine Liste, die jedem
Kontrollpunkt der Fläche einen Kontrollpunkt der Funktion zuweist.
Die Struktur ist grob in Abbildung 2.2
dargestellt. Details zur Implementierung des Algorithmus und der
Klassen stehen in Kapitel 4 und im Anhang A.
Die Struktur des Algorithmus' 1.2
ändert sich nicht.
bereits durch die Fläche bestimmt werden,
können hierfür die gleichen Formeln wie für die Flächenkontrollpunkte
verwendet werden. Dazu müssen wir den
Algorithmus 1.2 erweitern. Zusätzlich
muß zu jedem Flächenkontrollpunkt der Funktionskontrollpunkt gefunden
werden und das Bézierkontrollnetz für die Funktion analog zu dem für die
Fläche berechnet werden. Ein Funktionsobjekt stellen wir dabei durch
eine von Object abgeleitete Klasse Function dar. Sie
enthält einen Zeiger auf die zugehörige G-Spline-Fläche und auf die
Map Klasse. Die Map Klasse ist eine Liste, die jedem
Kontrollpunkt der Fläche einen Kontrollpunkt der Funktion zuweist.
Die Struktur ist grob in Abbildung 2.2
dargestellt. Details zur Implementierung des Algorithmus und der
Klassen stehen in Kapitel 4 und im Anhang A.
Die Struktur des Algorithmus' 1.2
ändert sich nicht.
Wird auf das Flächenkontrollnetz der Doo-Sabin-Algorithmus 1.3 angewendet, muß auch das Funktionskontrollnetz mit bearbeitet werden. Wie bei der Umwandlung in Bézierkontrollnetze müssen hier die gleichen Formeln auf die Kontrollpunkte der Funktion angewandt werden. Dazu wird der Algorithmus 1.3 so erweitert, daß er neben den Flächenkontrollpunkten auch gleich die Kontrollpunkte aller auf dieser Fläche definierten Funktionen in ein neues Kontrollnetz umwandelt.
Nachdem das Kontrollnetz der Funktion in Bézierkontrollnetze
umgewandelt worden ist, haben wir mehrere Möglichkeiten, die Funktion
darzustellen. Es bietet sich zunächst an, den Betrag des
Funktionswertes in eine Farbe umzuwandeln und die Fläche selbst
entsprechend einzufärben. Zu einem gegebenen Punkt ![]() auf der Fläche
berechnen wir den zugehörigen Farbwert
auf der Fläche
berechnen wir den zugehörigen Farbwert ![]() aus der über das
Bézierkontrollnetz berechneten Funktion. Für skalarwertige
Funktionen erhalten wir den Farbwert aus
aus der über das
Bézierkontrollnetz berechneten Funktion. Für skalarwertige
Funktionen erhalten wir den Farbwert aus
| (2.38) |
| (2.39) |
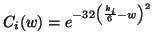 |
(2.40) |
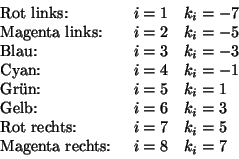 |
(2.41) |
![[R; G; B] = ... [r; 0; b] C_8(w)](img426.png) |
(2.42) |
![(u, v) -> [uv; u; v^2], u = -2:0.4:2, v = -2:0.4:2](img431.png) |
(2.43) |
| (2.44) |
Alternativ können wir die Funktionswerte auch durch Stacheln auf der Fläche darstellen. Dazu zeichnen wir eine Strecke vom einem Punkt
Die verschiedenen Darstellungsarten lassen sich auch miteinander verknüpfen und sie können mittels eines einzigen Alogrithmus' berechnet werden. Zu jedem biquadratischen Bézierkontrollnetz der Funktion suchen wir zunächst das zugehörige Bézierkontrollnetz der Fläche. Wird schon beim Erzeugen der Bézierkontrollnetze hierauf Rücksicht genommen, können die Kontrollnetze in der gleichen Reihenfolge in jeweils einer Liste abgelegt werden, so daß wir nur noch beide Listen gleichzeitig durchlaufen müssen. Wir legen dann ein Gitter über den Parameterbereich und je nach ausgewählter Darstellungsart berechnen wir den Punkt auf der Fläche, die Flächennormale und den Funktionswert an den Gitterknoten. Die Stacheln, Vektoren und Gitternetze können direkt als Linien dargestellt werden. Für die farbigen Flächen unterteilen wir jedes Quadrat in zwei Dreiecke. Über die Farbwerte an den Ecken lassen sich dann einfach die Farbverläufe auf den Dreiecken bestimmen.
Mit Hilfe der Stacheln kann man z.B. das Einheitsnormalenfeld einer Fläche darstellen. Dazu verwenden wir einfach eine konstante Funktion auf dieser Fläche. Abbildung 2.4 zeigt das Einheitsnormalenfeld einer Acht-Fläche. Die Kontrollpunkte der Fläche wurden durch
![(u , v) -> [cos(u) cos(v) sin(v); sin(u) cos(v) sin(v); sin(v)]](img439.png) für für |
(2.45) |
In Abbildung 2.6 stellen wir näherungsweise das Potential
eines statischen Dipols in der ![]() -
-![]() -Ebene dar. Die Fläche ist ist dabei
der durch die Kontrollpunkte
-Ebene dar. Die Fläche ist ist dabei
der durch die Kontrollpunkte
![]() mit
mit
![]() bestimmte Teil der
bestimmte Teil der ![]() -
-![]() -Ebene. Die Kontrollpunkte der
Potentialfunktion wurden durch die Funktion
-Ebene. Die Kontrollpunkte der
Potentialfunktion wurden durch die Funktion
| (2.46) |