2.3.1 Oberflächenintegrale

Next: 2.3.2 Bivariater Romberg-Algorithmus Up: 2.3 Integration Previous: 2.3 Integration Inhalt

2.3.1 Oberflächenintegrale

Wir wollen nun die über G-Spline-Kontrollpunkte gegebene Funktion auf der G-Spline-Fläche integrieren. Dazu betrachten wir zunächst die allgemeine Definition.

Definition 2.1 (Oberflächenintegral von Skalarfeldern) Es sei $S: R^2 \supset K -> R^3$ eine Fläche und

ein stetiges Skalarfeld auf

. Dann ist durch

$\int_S f d sigma := \int_K f(S(u,v)) |(\partial S)/(\partial u) x (\partial S)/(\partial v)| d(u,v)$

(2.47)

das Oberflächenintegral von

über

definiert (vgl. [Heu90]).

Wir nehmen an, daß für und die biquadratischen Bézierkontrollnetze bereits erzeugt wurden. Der Parameterbereich von sei ein aus kompakten Intervallen im zusammengesetztes Gebiet. Damit können wir in kompakte, zwei-dimensionale Intervalle der Form mit $a_i, b_i \in R$ und $i \in I$ zerlegen. Jedes ist der Parameterbereich eines Bézierflächenstücks. Dann gilt

$\int_S f d sigma = \sum_{i\in I} ...$

(2.48)

Wir betrachten jetzt speziell einen Parameterbereich . Die Funktion sei für durch ein in der Form von (2.36) mit $F^i_{j,k} \in R$ für gegeben,

$f_i: [0,1]^2 -> R, f_i(u,v) = \sum_{j=0}^2 \sum_{k=0}^2 F^i_{j,k} B^2_j(u) B^2_k(v).$

(2.49)

sei durch

$S_i: [0,1]^2 -> R, S_i(u,v) = \sum_{j=0}^2 \sum_{k=0}^2 P^i_{j,k} B^2_j(u) B^2_k(v)$

(2.50)

mit $P^i_{j,k} \in R^3$ gegeben. Beide Funktionen lassen sich durch eine einfache Translation $t_i: K_i \to [0,1]^2, (a,b) -> (a-a_i,b-b_i)$ von

auf

verschieben, so daß

und

für $(a,b) \in K_i$ gilt. Da

, erhalten wir für das Integral über

$\iint_{K_i} (S(a,b)) |...| d(u,v).$

(2.51)

Für das Integral (2.48) müssen wir also für jedes biquadratische Bézierflächenstück der Fläche bzw. der Funktion das Integral über (2.51) berechnen.

Im mehrdimensionalen Fall können wir natürlich zunächst über die Norm integrieren. Für drei-dimensionale Vektorfelder wollen wir aber speziell ein Oberflächenintegral durch die folgende Definition einführen.

Definition 2.2 (Oberflächenintegral von Vektorfeldern) Es sei $S: R^2 \supset K -> R^3, (u,v) -> [X(u,v), Y(u,v), Z(u,v)]^T$ eine Fläche mit dem Parameterbereich

und

(2.52)

ein stetiges drei-dimensionales Vektorfeld auf

. Dann definiert man

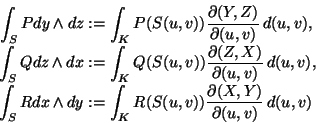$\int_S P dy \wedge dz := \int_K P(S(u,v)) ... d(u,v)$

(2.53)

und man nennt

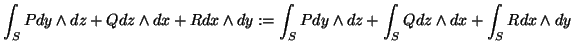$\int_S P dy \wedge dz + Q dz \wedge dx + R dx \wedge dy := \int_S P dy \wedge dz + \int_S Q dz \wedge dx + \int_S R dx \wedge dy$

(2.54)

das Oberflächenintegral von

über

. (vgl. [Heu90])

Dabei ist aber zu beachten, daß das Oberflächenintegral $\int_S P dy \wedge dz + Q dz \wedge dx + R dx \wedge dy$ auch von der Parameterdarstellung von abhängt. Es ist aber invariant unter positivem Parameterwechsel und ändert nur das Vorzeichen bei negativem Parameterwechsel. Es gibt eine zweite Möglichkeit, dieses Oberflächenintegral darzustellen (siehe z.B. [Heu90]). Ist der Einheitsnormalenvektor der Fläche an , dann können wir das Oberflächenintegral auch als

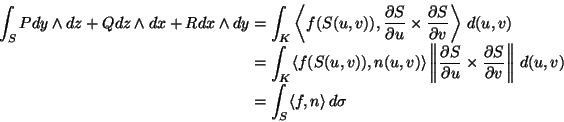$\int_S P dy \wedge dz + Q dz \wedge dx + R dx ... = \int_S <f,n> d sigma$

(2.55)

in der Form von (2.47) schreiben. Damit haben wir wieder ein skalares Oberflächenintegral, so daß wir für jedes Bézierflächenstück

mit $i \in I$ das Integral

$\iint_{[0,1]^2} <f_i,n> d(u,v)$

(2.56)

berechnen können, um das Oberflächenintegral des Vektorfeldes

zu erhalten.

Next: 2.3.2 Bivariater Romberg-Algorithmus Up: 2.3 Integration Previous: 2.3 Integration Inhalt

Copyright © 1999-2002 Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.1 or any later version published by the Free Software Foundation.

Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node20.html