


Next: 2.3.3 Flächeninhalt, Volumen, Schwerpunkt
Up: 2.3 Integration
Previous: 2.3.1 Oberflächenintegrale
Inhalt
Nachdem wir die beiden Formen der Oberflächenintegrale vorgestellt
haben und diese auf eine gemeinsame Form eines bivariaten Integrals
gebracht haben, werden wir eine Methode zur numerischen Berechnung
solcher bivariaten Integrale vorstellen. Siehe hierzu auch
[Höl98] und [KU98]. Zunächst führen wir dazu eine
univariate Integrationsformel für
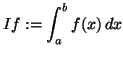 |
(2.57) |
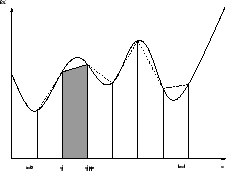
Abbildung 2.7:
Trapezregel
 |
ein. Zur numerischen Approximation dieses Integrals können wir 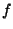 stückweise durch Polynome approximieren und die Integrale über diese
Polynome aufsummieren. Dazu zerlegen wir
stückweise durch Polynome approximieren und die Integrale über diese
Polynome aufsummieren. Dazu zerlegen wir ![[a,b]](img493.png) durch die
durch die 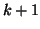 äquidistanten Stützstellen
äquidistanten Stützstellen
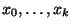 in
in 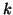 Teilintervalle,
Teilintervalle,
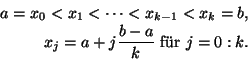 |
(2.58) |
Approximieren wir, wie in Abbildung 2.7 gezeigt, 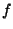 auf jedem Teilintervall durch eine lineare Funktion, erhalten wir nach
der Integration der linearen Funktionen die Trapezregel
auf jedem Teilintervall durch eine lineare Funktion, erhalten wir nach
der Integration der linearen Funktionen die Trapezregel 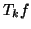 :
:
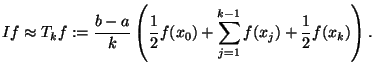 |
(2.59) |
Der Fehler der Trapezregel 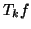 zum exakten Wert
läßt sich asymptotisch durch folgendes Theorem beschreiben.
zum exakten Wert
läßt sich asymptotisch durch folgendes Theorem beschreiben.
Theorem 2.3 (Euler-Maclaurin-Summationsformel)
Sei
![\in C^{2m}([a,b])](img500.png)
. Dann gilt
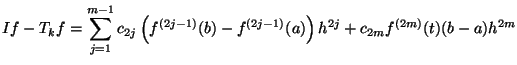 |
(2.60) |
für
![t\in[a,b]](img502.png)
und den von
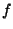
unabhängigen Konstanten
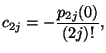 |
(2.61) |
die über die Bernoulli Polynome

definiert werden:
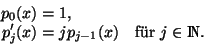 |
(2.62) |
Nach (2.60) kann der Fehler der Trapezregel durch
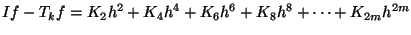 |
(2.63) |
dargestellt werden. Dabei ist
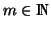 beliebig, solange
beliebig, solange
![f \in C^{2m}([a,b])](img500.png) . Die Konstanten
. Die Konstanten 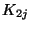 hängen dabei nicht von der
Schrittweite
hängen dabei nicht von der
Schrittweite 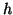 , sondern nur von
, sondern nur von 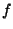 selbst ab. Damit lassen sich
einzelne Fehlerterme über die Richardson-Extrapolation eliminieren,
selbst ab. Damit lassen sich
einzelne Fehlerterme über die Richardson-Extrapolation eliminieren,
Mit der Trapezregel berechnen wir also zunächst 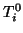 , wobei wir mit
, wobei wir mit
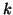 Punkten anfangen und diese pro Schritt in
Punkten anfangen und diese pro Schritt in 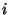 verdoppeln. Pro
Schritt in
verdoppeln. Pro
Schritt in 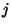 verschwindet in
verschwindet in 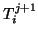 jeweils ein Fehlerterm
durch Kombination von
jeweils ein Fehlerterm
durch Kombination von 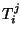 und
und 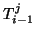 . Dieser Algorithmus wird
auch als Romberg-Algorithmus bezeichnet. Er läßt sich auch durch das
folgende Dreieckschema darstellen:
. Dieser Algorithmus wird
auch als Romberg-Algorithmus bezeichnet. Er läßt sich auch durch das
folgende Dreieckschema darstellen:
Aus diesem Algorithmus werden wir ein numerisches
Integrationsverfahren für bivariate Integrale
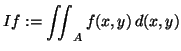 |
(2.65) |
herleiten. Für unsere Anwendung genügt es anzunehmen, daß 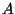 ein
zwei-dimensionales Intervall
ein
zwei-dimensionales Intervall
![[a,b] x [c,d]](img520.png) in
in
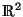 ist.
Wir unterteilen beide Intervalle
ist.
Wir unterteilen beide Intervalle ![[a,b]](img493.png) und
und ![[c,d]](img521.png) in jeweils
in jeweils 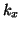 bzw.
bzw. 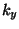 Teilintervalle und wenden die Trapezregel auf beide Integrale
getrennt an. Mit
Teilintervalle und wenden die Trapezregel auf beide Integrale
getrennt an. Mit
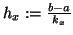 und
und
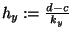 ergibt dies die numerische Integrationsformel
ergibt dies die numerische Integrationsformel
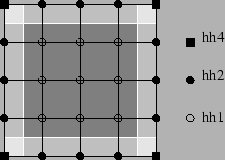
Abbildung 2.8:
Bivariate Trapezregel
 |
Damit erhalten wir eine bivariate Integrationsformel aus dem
Tensorprodukt der univariaten Trapezregel. Wir legen dazu ein
zwei-dimensionales Gitter mit den Schrittweiten 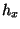 ,
, 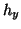 über das
rechteckige Integrationsgebiet und multiplizieren die Funktionswerte
an den Knoten mit bestimmten Faktoren. Dabei müssen wir zwischen
Eckknoten, Randknoten und inneren Knoten unterscheiden. Die Faktoren
aus der Formel (2.66) sind in Abbildung 2.8
dargestellt.
über das
rechteckige Integrationsgebiet und multiplizieren die Funktionswerte
an den Knoten mit bestimmten Faktoren. Dabei müssen wir zwischen
Eckknoten, Randknoten und inneren Knoten unterscheiden. Die Faktoren
aus der Formel (2.66) sind in Abbildung 2.8
dargestellt.
Den Fehler für (2.66) können wir durch zweimaliges Anwenden von
Theorem 2.3 bestimmen. Danach gilt für
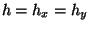
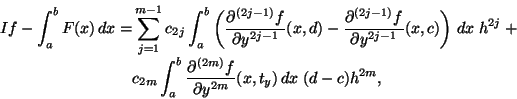 |
(2.67) |
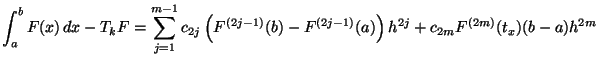 |
(2.68) |
mit
![t_x \in [a,b]](img536.png) und
und
![t_y \in [c,d]](img537.png) . Uns interessiert aber nur
die allgemeine Form des Fehlers und dieser enthält wieder nur Terme
mit
. Uns interessiert aber nur
die allgemeine Form des Fehlers und dieser enthält wieder nur Terme
mit 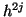 ,
,
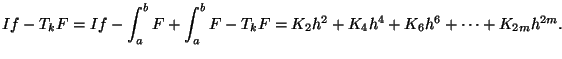 |
(2.69) |
Dabei hängen die 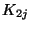 nur von
nur von 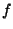 ab. Dies
entspricht (2.63) und wir können damit den
Romberg-Algorithmus (2.64) auch für die bivariate
Trapezregel verwenden.
ab. Dies
entspricht (2.63) und wir können damit den
Romberg-Algorithmus (2.64) auch für die bivariate
Trapezregel verwenden.
Nun können wir den allgemeinen Algorithmus zur Berechnung eines
Integrals einer G-Spline-Funktion über einer G-Spline-Fläche der
Form
![\sum_{i\in I} \iint_{[0,1]^2} F_i](img540.png) |
(2.70) |
angeben. Wir gehen davon aus, daß die Fläche bereits über
Bézierflächenstücke 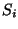 für
für 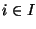 gegeben ist. Die Funktion
wird auf jedem Bézierflächenstück
gegeben ist. Die Funktion
wird auf jedem Bézierflächenstück 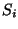 durch
durch 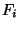 repräsentiert.
repräsentiert.
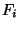 kann dabei wie oben beschrieben über ein Bézierkontrollnetz
gegeben sein. Es kann aber auch nur von der Oberfläche selbst
abhängen. Wir müssen nur jeweils die Trapezregel, bzw. die in der
Trapezregel verwendete Funktion entsprechend wählen. Für die bisher
vorgestellten Integrale geht dies aus den
Formeln (2.51) und (2.56) hervor.
kann dabei wie oben beschrieben über ein Bézierkontrollnetz
gegeben sein. Es kann aber auch nur von der Oberfläche selbst
abhängen. Wir müssen nur jeweils die Trapezregel, bzw. die in der
Trapezregel verwendete Funktion entsprechend wählen. Für die bisher
vorgestellten Integrale geht dies aus den
Formeln (2.51) und (2.56) hervor.
Algorithmus 2.1
| integrate |
| Bivariater Romberg-Algorithmus |
- 1.
- Setze das Ergebnis value der Integration auf 0.
- 2.
- Berechne das Integral für jedes Bézierkontrollnetz bgs der
G-Spline-Fläche separat über den Romberg-Algorithmus:
- (a)
- Initialisiere die Variablen für den Romberg-Algorithmus.
Dabei ist t ein Array der Länge max_iter,
welche die maximale Anzahl der Iterationen angibt. n
gibt die Anzahl der Stützstellen in einer Gitterrichtung an und
i wird als Iterationszähler auf 1 gesetzt.
- (b)
- Berechne die Trapezregel für die Intervalllänge 1/(n-1)
pro Gitterrichtung (
n
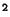 Stützstellen) und lege das Ergebnis in t[0] ab.
Stützstellen) und lege das Ergebnis in t[0] ab.
- (c)
- Wiederhole Folgendes, solange die gewünschte Toleranz
prec nicht erreicht wurde oder die maximale Anzahl der
Iterationen erreicht wurde:
- i.
- Verdopple n.
- ii.
- Berechne die Trapezregel für die Intervalllänge 1/(n-1)
pro Gitterrichtung (
n
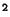 Stützstellen) und lege das Ergebnis in t[i] ab.
Stützstellen) und lege das Ergebnis in t[i] ab.
- iii.
- Für j = i:-1:1 berechne die Romberg-Extrapolation
iterativ über
t[j-1] = (4
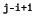 *
t[j] - t[j-1]) / (4
*
t[j] - t[j-1]) / (4
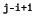 - 1).
- 1).
- iv.
- Zur Bestimmung der Genauigkeit berechne den Betrag
der Differenz zwischen dem besten Wert der Extrapolation in
t[0] und dem besten Ergebnis der vorherigen Iteration.
- v.
- Erhöhe i um 1.
- (d)
- Addiere das Ergebnis des Romberg-Algorithmus' zu value.
- 3.
- Das Ergebnis der Integration steht in value.
Es ist zunächst zu beachten, daß wir das Array t von rechts
nach links füllen. Damit benötigen wir nur ein einziges,
eindimensionales Array für die Extrapolation, in dem aus den alten
Werten die neuen berechnet werden. Im ersten Schritt wird das
Ergebnis der Trapezregel in ein noch nicht benutztes Element
t[i] des Arrays abgelegt und die Extrapolationswerte von
diesem Element aus bis t[0] eingetragen.
Die im Algorithmus verwendete Toleranz prec bezieht sich
dabei auf das Integral über eine einzelne Bézierfläche. Durch
das Aufsummieren der Ergebnisse verringert sich die Toleranz
für das gesamte Integral. Bei 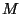 Bézierflächen ist sie nur noch
Bézierflächen ist sie nur noch
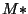 prec.
prec.
Die verwendete Trapezregel entspricht natürlich der bivariaten
Trapezregel (2.66), wobei im Algorithmus die Anzahl der
Intervalle 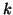 durch die Anzahl der Stützstellen
durch die Anzahl der Stützstellen 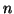 ersetzt wurde. Es
gilt
ersetzt wurde. Es
gilt 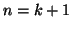 . Je nach Integral kann
. Je nach Integral kann 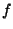 durch andere Funktionen
ersetzt werden. So verwenden wir z.B. für das Oberflächenintegral von
Vektorfeldern die Funktion
durch andere Funktionen
ersetzt werden. So verwenden wir z.B. für das Oberflächenintegral von
Vektorfeldern die Funktion
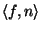 . Spezielle Integrale
stellen wir weiter unten vor.
. Spezielle Integrale
stellen wir weiter unten vor.
Abbildung 2.9:
Funktionsauswertungen bei der bivariaten Trapezregel
 |
Weiter ist auch zu beachten, daß wir nach dem ersten Auswerten der
Trapezregel für die folgenden Auswertungen die Funktion nicht mehr an
allen Stützpunkten berechnen müssen. Nachdem wir 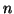 jeweils
verdoppeln, benötigen wir nur noch die Stützstellen
jeweils
verdoppeln, benötigen wir nur noch die Stützstellen
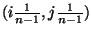 , bei denen wenigstens eine der beiden
Zahlen
, bei denen wenigstens eine der beiden
Zahlen 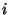 und
und 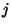 ungerade ist. Für die restlichen Stützstellen
können wir das Ergebnis der vorherigen Trapezregel mit
ungerade ist. Für die restlichen Stützstellen
können wir das Ergebnis der vorherigen Trapezregel mit
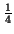 multiplizieren. Die Punkte, an denen die Funktion noch ausgewertet
werden muß, sind in Abbildung 2.9 gekennzeichnet.
Von den
multiplizieren. Die Punkte, an denen die Funktion noch ausgewertet
werden muß, sind in Abbildung 2.9 gekennzeichnet.
Von den 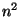 Stützstellen wird die Funktion dann nur noch an
Stützstellen wird die Funktion dann nur noch an
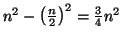 Stützstellen berechnet.
Stützstellen berechnet.
Eine mögliche Verbesserung des Romberg-Algorithmus' wäre eine
adaptive Anpassung an den Approximationsfehler. Wir berechnen dazu
zunächst das Integral für ein zwei-dimensionales
Integrationsintervall 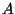 und schätzen zusätzlich den Fehler des
Ergebnisses ab. Ist dieser Fehler größer als eine vorgegebene Toleranz
und schätzen zusätzlich den Fehler des
Ergebnisses ab. Ist dieser Fehler größer als eine vorgegebene Toleranz
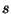 , unterteilen wir das Intervall
, unterteilen wir das Intervall 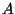 in vier gleichgroße
Teilintervalle und berechnen für diese Intervalle das Integral
getrennt mit der Toleranz
in vier gleichgroße
Teilintervalle und berechnen für diese Intervalle das Integral
getrennt mit der Toleranz
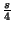 . Dies wird rekursiv
wiederholt, bis die Fehlerabschätzung kleiner als die Toleranz ist.
Hierdurch wird die Anzahl der Stützstellen dem jeweiligen
Approximationsfehler auf dem Teilintervall angepaßt. Nachdem wir aber
schon das Integrationsgebiet am Anfang in die einzelnen quadratischen
Bézierfläche unterteilen, haben wir den adaptiven Algorithmus nicht
implementiert.
. Dies wird rekursiv
wiederholt, bis die Fehlerabschätzung kleiner als die Toleranz ist.
Hierdurch wird die Anzahl der Stützstellen dem jeweiligen
Approximationsfehler auf dem Teilintervall angepaßt. Nachdem wir aber
schon das Integrationsgebiet am Anfang in die einzelnen quadratischen
Bézierfläche unterteilen, haben wir den adaptiven Algorithmus nicht
implementiert.



Next: 2.3.3 Flächeninhalt, Volumen, Schwerpunkt
Up: 2.3 Integration
Previous: 2.3.1 Oberflächenintegrale
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node21.html
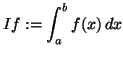
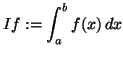
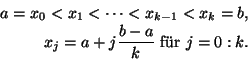
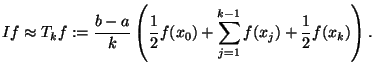
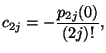
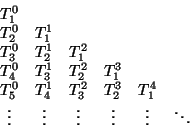
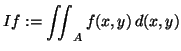
![]()
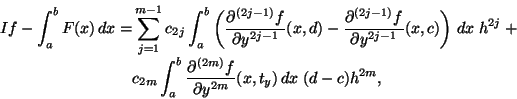
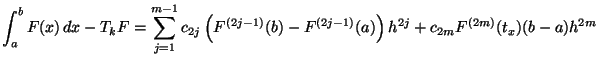
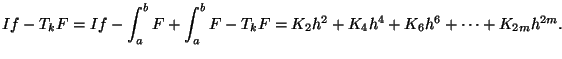
![\sum_{i\in I} \iint_{[0,1]^2} F_i](img540.png)
![]() Bézierflächen ist sie nur noch
Bézierflächen ist sie nur noch
![]() prec.
prec.
![]() durch die Anzahl der Stützstellen
durch die Anzahl der Stützstellen ![]() ersetzt wurde. Es
gilt
ersetzt wurde. Es
gilt ![]() . Je nach Integral kann
. Je nach Integral kann ![]() durch andere Funktionen
ersetzt werden. So verwenden wir z.B. für das Oberflächenintegral von
Vektorfeldern die Funktion
durch andere Funktionen
ersetzt werden. So verwenden wir z.B. für das Oberflächenintegral von
Vektorfeldern die Funktion
![]() . Spezielle Integrale
stellen wir weiter unten vor.
. Spezielle Integrale
stellen wir weiter unten vor.
![]() und schätzen zusätzlich den Fehler des
Ergebnisses ab. Ist dieser Fehler größer als eine vorgegebene Toleranz
und schätzen zusätzlich den Fehler des
Ergebnisses ab. Ist dieser Fehler größer als eine vorgegebene Toleranz
![]() , unterteilen wir das Intervall
, unterteilen wir das Intervall ![]() in vier gleichgroße
Teilintervalle und berechnen für diese Intervalle das Integral
getrennt mit der Toleranz
in vier gleichgroße
Teilintervalle und berechnen für diese Intervalle das Integral
getrennt mit der Toleranz
![]() . Dies wird rekursiv
wiederholt, bis die Fehlerabschätzung kleiner als die Toleranz ist.
Hierdurch wird die Anzahl der Stützstellen dem jeweiligen
Approximationsfehler auf dem Teilintervall angepaßt. Nachdem wir aber
schon das Integrationsgebiet am Anfang in die einzelnen quadratischen
Bézierfläche unterteilen, haben wir den adaptiven Algorithmus nicht
implementiert.
. Dies wird rekursiv
wiederholt, bis die Fehlerabschätzung kleiner als die Toleranz ist.
Hierdurch wird die Anzahl der Stützstellen dem jeweiligen
Approximationsfehler auf dem Teilintervall angepaßt. Nachdem wir aber
schon das Integrationsgebiet am Anfang in die einzelnen quadratischen
Bézierfläche unterteilen, haben wir den adaptiven Algorithmus nicht
implementiert.