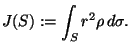


Next: 2.4 Isolinien
Up: 2.3 Integration
Previous: 2.3.2 Bivariater Romberg-Algorithmus
Inhalt
Wir betrachten noch zwei spezielle Integrale für G-Spline-Flächen.
Der Flächeninhalt 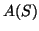 einer Fläche
einer Fläche 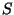 ist definiert durch
ist definiert durch
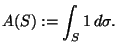 |
(2.71) |
Für den Flächeninhalt der G-Spline-Fläche genügt es somit, das Integral
![\iint_{[0,1]^2} |(\partial S_i)/(\partial u) x (\partial S_i)/(\partial v)| d(u,v).](img556.png) |
(2.72) |
pro Bézierfläche
![S_i: [0,1]^2 -> R^3](img557.png) zu berechnen. Dies läßt
sich durch eine einfache Änderung der Trapezregel im
Romberg-Algorithmus implementieren.
zu berechnen. Dies läßt
sich durch eine einfache Änderung der Trapezregel im
Romberg-Algorithmus implementieren.
Für eine geschlossene G-Spline-Fläche können wir auch das Volumen
berechnen. Für das Volumenintegral einer Fläche 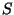 , welche das Volumen
, welche das Volumen
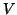 einschließt, gilt nach dem Gauß'schen Integrationssatz, daß
einschließt, gilt nach dem Gauß'schen Integrationssatz, daß
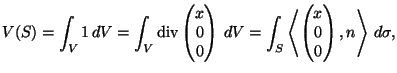 |
(2.73) |
wobei 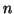 der nach außen gerichtete Einheitsnormalenvektor von
der nach außen gerichtete Einheitsnormalenvektor von 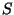 ist. Analog erhält man für das Volumenintegral auch die Formeln
ist. Analog erhält man für das Volumenintegral auch die Formeln
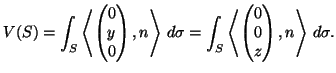 |
(2.74) |
Daraus folgt
![V(S) = 1/3 \int_{S} <([x;y;z]), n> d sigma.](img561.png) |
(2.75) |
Dies entspricht dem Oberflächenintegral des Vektorfeldes
![[x, y, z]^T](img562.png) . Nachdem in dieser Formel alle
drei Koordinaten vorkommen, ist sie auch numerisch stabiler. Für
geschlossene G-Spline-Flächen erhalten wir das Volumen damit aus
der Summe der Integrale
. Nachdem in dieser Formel alle
drei Koordinaten vorkommen, ist sie auch numerisch stabiler. Für
geschlossene G-Spline-Flächen erhalten wir das Volumen damit aus
der Summe der Integrale
![1/3 \iint_{[0,1]^2} < S_i, N > d(u,v)](img563.png) |
(2.76) |
pro Bézierfläche 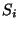 , wobei
, wobei 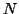 der nach außen gerichtete
Normalenvektor der Fläche ist. Durch eine entsprechende Änderung der
Trapezregel können wir so auch das Volumen berechnen. Dabei überprüfen
wir allerdings nicht, ob die Fläche geschlossen ist und damit das
Volumen überhaupt existiert. In wieweit das berechnete Integral
definiert ist, bleibt dem Benutzer überlassen.
der nach außen gerichtete
Normalenvektor der Fläche ist. Durch eine entsprechende Änderung der
Trapezregel können wir so auch das Volumen berechnen. Dabei überprüfen
wir allerdings nicht, ob die Fläche geschlossen ist und damit das
Volumen überhaupt existiert. In wieweit das berechnete Integral
definiert ist, bleibt dem Benutzer überlassen.
Abbildung 2.10:
Volumenintegral für die Fläche aus der Abbildung 1.19 (einfacher Würfel)
 |
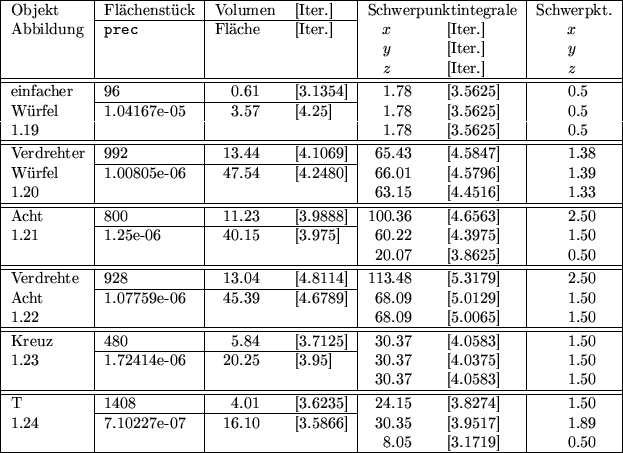
Abbildung 2.11:
Integrale und Flächenschwerpunkte verschiedener Objekte
 |
Die Tabelle in Abbildung 2.10 enthält die
Ergebnisse der Volumenberechnung des einfachen Würfels aus
Abbildung 1.19 für verschiedene Toleranzwerte. Zum
Vergleich geben wir neben den Ergebnissen des Romberg-Algorithmus'
auch die der bivariaten Trapezregel an. Die Iterationen sind die
mittlere Anzahl der Iterationen, die für ein Flächenstück benötigt
wurden, um die gewünschte Genauigkeit zu erreichen. Der Würfel besteht
aus 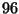 Flächenstücken, d.h. die gesamte Toleranz ist
Flächenstücken, d.h. die gesamte Toleranz ist 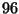 mal
größer als die Toleranz für die einzelnen Flächenstücke. Man sieht an
der Tabelle, daß die mittlere Anzahl der Iterationen für die
Trapezregel schneller als für den Romerg-Algorithmus mit dem
Verkleinern der Toleranzwerte steigt.
mal
größer als die Toleranz für die einzelnen Flächenstücke. Man sieht an
der Tabelle, daß die mittlere Anzahl der Iterationen für die
Trapezregel schneller als für den Romerg-Algorithmus mit dem
Verkleinern der Toleranzwerte steigt.
Mit Hilfe der vorgestellten Integrationsalgorithmen können wir den
Schwerpunkt einer Fläche 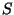 berechnen. Sei dazu
berechnen. Sei dazu
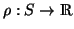 die
Flächendichte von
die
Flächendichte von 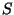 . Dann ist die Masse von
. Dann ist die Masse von 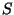
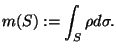 |
(2.77) |
Der Schwerpunkt 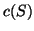 ist
ist
![c(S) := 1/m(S) ([\int_S x rho d sigma; \int_S y rho d sigma; \int_S z rho d sigma]).](img571.png) |
(2.78) |
Für
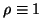 zeigt die Tabelle in
Abbildung 2.11 das Volumen, den Flächeninhalt, der
hier physikalisch der Masse der Fläche entspricht, die obigen drei
Integrale für den Schwerpunkt und die Koordinaten des Schwerpunktes
für die im Kapitel 1 vorgestellten Flächen. Die
Toleranzen wurden so gewählt, daß die gesamte Toleranz in etwa
zeigt die Tabelle in
Abbildung 2.11 das Volumen, den Flächeninhalt, der
hier physikalisch der Masse der Fläche entspricht, die obigen drei
Integrale für den Schwerpunkt und die Koordinaten des Schwerpunktes
für die im Kapitel 1 vorgestellten Flächen. Die
Toleranzen wurden so gewählt, daß die gesamte Toleranz in etwa 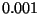 beträgt. Die in eckigen Klammern angegebenen Werte entsprechen der
mittleren Anzahl der Iterationen pro Flächenstück. Es sei auch darauf
hingewiesen, daß der Integrand für die Schwerpunktintegrale durch eine
G-Spline-Funktion angegeben wurde.
beträgt. Die in eckigen Klammern angegebenen Werte entsprechen der
mittleren Anzahl der Iterationen pro Flächenstück. Es sei auch darauf
hingewiesen, daß der Integrand für die Schwerpunktintegrale durch eine
G-Spline-Funktion angegeben wurde.
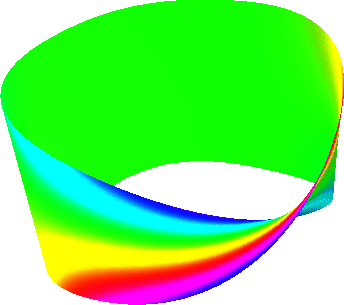
Abbildung 2.12:
Trägheitsmoment eines Möbiusbandes
 |
Wir können ebenfalls das Trägheitsmoment 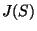 einer Fläche
einer Fläche 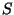 mit
der Dichte
mit
der Dichte 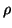 bzgl. einer Rotationsachse berechnen,
bzgl. einer Rotationsachse berechnen,
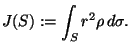 |
(2.79) |
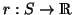 weist jedem Punkt der Fläche seinen senkrechten Abstand
zu der Rotationsachse zu. Dabei geben wir
weist jedem Punkt der Fläche seinen senkrechten Abstand
zu der Rotationsachse zu. Dabei geben wir 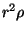 wieder als
G-Spline-Funktion auf der Fläche an. Für das Möbiusband aus
Abbildung 1.16 mit der Dichte
wieder als
G-Spline-Funktion auf der Fläche an. Für das Möbiusband aus
Abbildung 1.16 mit der Dichte
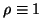 ist das
Trägheitsmoment um die Mittelachse gleich
ist das
Trägheitsmoment um die Mittelachse gleich 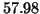 bei einem
Flächeninhalt von
bei einem
Flächeninhalt von 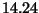 . Je weiter die einzelnen Masseteilchen der
Fläche von der Rotationsachse entfernt sind, um so stärker wirken sie
sich auf die Rotation aus. Die Funktion
. Je weiter die einzelnen Masseteilchen der
Fläche von der Rotationsachse entfernt sind, um so stärker wirken sie
sich auf die Rotation aus. Die Funktion 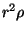 ist für das
Möbiusband in Abbildung 2.12 dargestellt. Nachdem
das Möbiusband nicht orientierbar ist, eignet sich die reine
Farbdarstellung der Funktion am besten.
ist für das
Möbiusband in Abbildung 2.12 dargestellt. Nachdem
das Möbiusband nicht orientierbar ist, eignet sich die reine
Farbdarstellung der Funktion am besten.



Next: 2.4 Isolinien
Up: 2.3 Integration
Previous: 2.3.2 Bivariater Romberg-Algorithmus
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node22.html
![]() einer Fläche
einer Fläche ![]() ist definiert durch
ist definiert durch
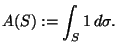
![\iint_{[0,1]^2} |(\partial S_i)/(\partial u) x (\partial S_i)/(\partial v)| d(u,v).](img556.png)
![]() , welche das Volumen
, welche das Volumen
![]() einschließt, gilt nach dem Gauß'schen Integrationssatz, daß
einschließt, gilt nach dem Gauß'schen Integrationssatz, daß
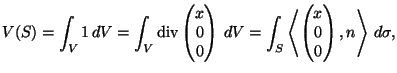
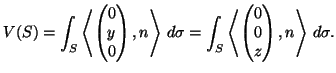
![V(S) = 1/3 \int_{S} <([x;y;z]), n> d sigma.](img561.png)
![1/3 \iint_{[0,1]^2} < S_i, N > d(u,v)](img563.png)
![]() Flächenstücken, d.h. die gesamte Toleranz ist
Flächenstücken, d.h. die gesamte Toleranz ist ![]() mal
größer als die Toleranz für die einzelnen Flächenstücke. Man sieht an
der Tabelle, daß die mittlere Anzahl der Iterationen für die
Trapezregel schneller als für den Romerg-Algorithmus mit dem
Verkleinern der Toleranzwerte steigt.
mal
größer als die Toleranz für die einzelnen Flächenstücke. Man sieht an
der Tabelle, daß die mittlere Anzahl der Iterationen für die
Trapezregel schneller als für den Romerg-Algorithmus mit dem
Verkleinern der Toleranzwerte steigt.
![]() berechnen. Sei dazu
berechnen. Sei dazu
![]() die
Flächendichte von
die
Flächendichte von ![]() . Dann ist die Masse von
. Dann ist die Masse von ![]()
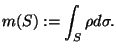
![c(S) := 1/m(S) ([\int_S x rho d sigma; \int_S y rho d sigma; \int_S z rho d sigma]).](img571.png)