


Next: 3.2 Funktionen auf getrimmten
Up: 3. Getrimmte Flächen
Previous: 3. Getrimmte Flächen
Inhalt
Abbildung 3.1:
ImplicitFunction Klasse
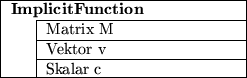 |
Wir können Flächen sowohl durch die Beschreibung von Gebieten im
Parameterbereich als auch durch die Angabe von Volumina im Raum der
Fläche trimmen. Haben wir dann eine Testfunktion, mit der wir
überprüfen können, ob die Parameter bzw. die Bildpunkte innerhalb
oder außerhalb dieser Bereiche liegen, können wir die getrimmten
Flächen darstellen.
Eine einfache, leicht zu implementierende Methode die Fläche im Raum
mit Hilfe von Volumina zu trimmen, besteht in der impliziten
Beschreibung der Volumina. Wir beschränken uns dazu auf die
quadratische Form
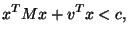 |
(3.1) |
wobei die 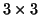 Matrix
Matrix 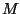 , der drei-dimensionale Vektor
, der drei-dimensionale Vektor 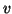 und
und
 beliebig gewählt werden können. Der so beschriebene
Körper wird durch die quadratische Fläche
beliebig gewählt werden können. Der so beschriebene
Körper wird durch die quadratische Fläche
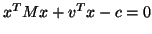 begrenzt, wobei für quadratische Flächen
begrenzt, wobei für quadratische Flächen  eine symmetrische Matrix
sein muß. Der Test, ob ein Punkt
eine symmetrische Matrix
sein muß. Der Test, ob ein Punkt 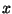 der Fläche in dem Volumen liegt,
besteht einfach darin, die Gleichung (3.1) zu überprüfen.
Eine solche quadratische, implizite Trimmfunktion beschreiben wir
durch die in Abbildung 3.1 dargestellte
Klasse ImplicitFunction. Man kann auch beliebige implizite
Funktionen, die Volumina im
der Fläche in dem Volumen liegt,
besteht einfach darin, die Gleichung (3.1) zu überprüfen.
Eine solche quadratische, implizite Trimmfunktion beschreiben wir
durch die in Abbildung 3.1 dargestellte
Klasse ImplicitFunction. Man kann auch beliebige implizite
Funktionen, die Volumina im
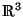 beschreiben, verwenden. Dabei würde
sich nur (3.1) im Algorithmus ändern.
beschreiben, verwenden. Dabei würde
sich nur (3.1) im Algorithmus ändern.
Im Parameterbereich geben wir die Trimmbereiche über Trimmkurven an.
Diese schneiden Teile des Parameterbereiches aus, die wir auf die
Fläche übertragen. Eine solche Trimmkurve beschreiben wir durch die
Klasse TrimCurve aus Abbildung 3.2. Eine
Trimmkurve beschreibt einen Trimmbereich für ein einzelnes
Bézierflächenstück der G-Spline-Fläche. Die Kurve kann entweder ein
Polygonzug oder eine geometrisch glatte, quadratische Splinekurve
sein. Der Parameterbereich sei wie üblich ![[0,1]^2](img589.png) . Die Trimmkurve
kann diesen Bereich aber verlassen.
. Die Trimmkurve
kann diesen Bereich aber verlassen.
Abbildung 3.2:
TrimCurve Klasse
 |
Für einen Polygonzug legen die Kontrollpunkte die Ecken fest. Zwei
aufeinanderfolgende Kontrollpunkte geben jeweils eine Linie des
Polygonzuges an. Zusätzlich wird der erste und der letzte Punkt in der
Kontrollpunktliste durch eine Linie miteinander verbunden. Der von
diesem Polygonzug eingeschlossene Bereich wird aus dem
Parameterbereich ausgeschnitten. Wir gehen dabei davon aus, daß der
Polygonzug immer im Uhrzeigersinn durchlaufen wird und alles, was
rechts vom Polygonzug liegt, ausgeschnitten wird. Einen
Testalgorithmus, mit dem wir bestimmen können, ob ein Punkt im
Parameterbereich ausgeschnitten wird, werden wir weiter unten
vorstellen.
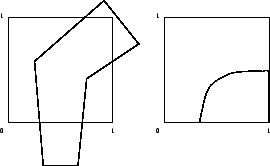
Abbildung 3.3:
Trimmkurven
 |
Geben die Kontrollpunkte eine quadratische Splinekurve an, dann gibt
es pro Kontrollpunkt 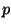 jeweils ein quadratisches
Bézierkurvensegment. Die für dieses Segment notwendigen drei
Bézierpunkte werden aus dem Kontrollpunkt
jeweils ein quadratisches
Bézierkurvensegment. Die für dieses Segment notwendigen drei
Bézierpunkte werden aus dem Kontrollpunkt 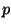 und dem Kontrollpunkt
vor und nach
und dem Kontrollpunkt
vor und nach 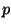 über die Bedingungen der geometrischen Stetigkeit
berechnet. Ist der erste und letzte Kontrollpunkt identisch, dann ist
die Kurve geschlossen. Ist die Kurve nicht geschlossen, dann erweitern
wir die Kurve zunächst so, daß Anfangs- und Endpunkt sicher außerhalb
des Parameterbereiches liegen und fügen Teile des Randes von
über die Bedingungen der geometrischen Stetigkeit
berechnet. Ist der erste und letzte Kontrollpunkt identisch, dann ist
die Kurve geschlossen. Ist die Kurve nicht geschlossen, dann erweitern
wir die Kurve zunächst so, daß Anfangs- und Endpunkt sicher außerhalb
des Parameterbereiches liegen und fügen Teile des Randes von ![[0,1]^2](img589.png) hinzu, damit eine geschlossene Kurve entsteht. Die so erzeugte
quadratische Kurve wandeln wir in einen Polygonzug um. Der eigentliche
Testalgorithmus ist dann mit dem für die Polygonzüge identisch.
Allgemein kann man natürlich eine Splinekurve von beliebigem Grad in
einen Polygonzug umwandeln.
hinzu, damit eine geschlossene Kurve entsteht. Die so erzeugte
quadratische Kurve wandeln wir in einen Polygonzug um. Der eigentliche
Testalgorithmus ist dann mit dem für die Polygonzüge identisch.
Allgemein kann man natürlich eine Splinekurve von beliebigem Grad in
einen Polygonzug umwandeln.
Abbildung 3.4:
Erweiterung der Trimmkurven
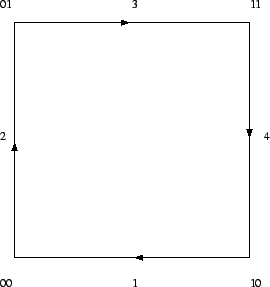 TD> TD> |
Abbildung 3.3 zeigt zwei Beispiele von Trimmkurven
im Parameterbereich. Wir berücksichtigen dabei noch nicht den
Umlaufsinn und mehrere Trimmkurven in einem Parameterbereich. Die
linke Trimmkurve ist ein Polygonzug. Dieser kann auch außerhalb des
Parameterbereiches fortgesetzt werden. Dies entspricht einer linearen
Trimmkurve im Parameterbereich, die entsprechende Teile des Randes von
![[0,1]](img471.png) enthält. Die rechte Trimmkurve wird durch eine Bézierkurve
bestimmt. Sie ist nicht geschlossen und wird durch den Rand von
enthält. Die rechte Trimmkurve wird durch eine Bézierkurve
bestimmt. Sie ist nicht geschlossen und wird durch den Rand von
![[0,1]^2](img589.png) erweitert. Wie dies genau geschieht wird im Algorithmus zur
Umwandlung in einen Polygonzug beschrieben. Liegt der Anfangs- oder
Endpunkt innerhalb des Parameterbereiches, verlängern wir zunächst die
Kurve in Richtung der Tangente an den entsprechenden Punkt, bis wir
den Parameterbereich verlassen haben. Danach verbinden wir den
Eintritts- und Austrittspunkt der Kurve aus dem Parameterbereich über
den Rand. Wir gehen dabei im Uhrzeigersinn vom Austrittspunkt zum
Eintrittspunkt.
erweitert. Wie dies genau geschieht wird im Algorithmus zur
Umwandlung in einen Polygonzug beschrieben. Liegt der Anfangs- oder
Endpunkt innerhalb des Parameterbereiches, verlängern wir zunächst die
Kurve in Richtung der Tangente an den entsprechenden Punkt, bis wir
den Parameterbereich verlassen haben. Danach verbinden wir den
Eintritts- und Austrittspunkt der Kurve aus dem Parameterbereich über
den Rand. Wir gehen dabei im Uhrzeigersinn vom Austrittspunkt zum
Eintrittspunkt.
Die Umwandlung dieser Kurven in Polygonzüge und die
Erweiterung durch den Rand des Parameterbereiches wird durch den
Algorithmus process_quadratic_trimcurve behandelt. Er
wandelt eine zwei-dimensionale quadratische Splinekurve mit n
Kontrollpunkten
b[0] b[n-1]
in einen Polygonzug
b[n-1]
in einen Polygonzug
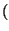 x[0]
x[0]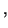 y[0]
y[0]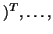
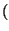 x[N-1]
x[N-1]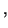 y[N-1]
y[N-1]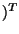 um. Dabei ist zu beachten, daß wir aus den Kontrollpunkten zunächst
die Bézierpunkte für eine geometrisch glatte, quadratische Kurve
berechnen. Für jedes quadratische Segment der Trimmkurve benötigen wir
um. Dabei ist zu beachten, daß wir aus den Kontrollpunkten zunächst
die Bézierpunkte für eine geometrisch glatte, quadratische Kurve
berechnen. Für jedes quadratische Segment der Trimmkurve benötigen wir
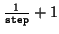 Linien, wenn step die
Schrittweite zur Berechnung der quadratischen Kurve ist. Wenn wir
die Kurve mit dem Rand von
Linien, wenn step die
Schrittweite zur Berechnung der quadratischen Kurve ist. Wenn wir
die Kurve mit dem Rand von ![[0,1]^2](img589.png) erweitern müssen, kommen noch
maximal vier Ecken hinzu. Für die Punkte, an denen wir das
Einheitsquadrat für die Erweiterung verlassen und eintreten, haben
wir nochmal zwei zusätzliche Punkte für den Polygonzug. Insgesamt ist
erweitern müssen, kommen noch
maximal vier Ecken hinzu. Für die Punkte, an denen wir das
Einheitsquadrat für die Erweiterung verlassen und eintreten, haben
wir nochmal zwei zusätzliche Punkte für den Polygonzug. Insgesamt ist
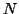 also nicht größer als
also nicht größer als
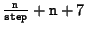 .
.
Algorithmus 3.1
| process_quadratic_trimcurve |
| Quadratische Trimmkurve in einen Polygonzug umwandeln |
- 1.
- Initialisiere die Arrays x und y für
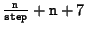 Punkte des Polygonzuges.
Punkte des Polygonzuges.
- 2.
- Berechne für jeweils drei aufeinanderfolgende Kontrollpunkte
b0, b2, b4 der Trimmkurve den Polygonzug:
- (a)
- Die Bézierpunkte der quadratischen Kurve sind b1,
b2 und b3, wobei b1 das Mittel von
b0 und b2 ist und b3 das Mittel von
b2 und b4.
- (b)
- Berechne den Polygonzug der Bézierkurve nach
Definition 1.4. Dazu unterteile das Intervall
![[0,1]](img471.png) mit der Schrittweite step und hänge die Koordinaten der
neuen Punkte an die Arrays x und y an.
mit der Schrittweite step und hänge die Koordinaten der
neuen Punkte an die Arrays x und y an.
- (c)
- Bestimme die nächsten drei Kontrollpunkte unter Berücksichtigung
möglicher Erweiterungen durch den Rand des Parameterbereiches:
- i.
- Zunächst wird b0 der Punkt b2 und b2
der Punkt b4 zugewiesen. b4 wird der nächste, noch
nicht benutzte Punkt aus der Kontrollpunktliste.
- ii.
- Existiert b4, dann kann die Umwandlung fortgesetzt werden.
- iii.
- Existiert b4 nicht, dann überprüfe, ob die Kurve
geschlossen ist. Dazu muß der erste und der letzte Kontrollpunkt
(also hier b2 und der erste Punkt in der
Kontrollpunktliste) gleich sein. Ist dies der Fall, dann setze
b4 auf den zweiten Kontrollpunkt in der Liste und
wandle diese letzte Kurve in einen Polygonzug um. Ansonsten
erweitere die Kurve mit dem Rand des Parameterbereiches, da die
Kurve nicht geschlossen ist:
- a.
- Liegt der zuletzt berechnete Punkt noch innerhalb des
Parameterbereiches, dann füge einen neuen Punkt hinzu, indem
zum letzten Punkt der Vektor, der die letzte Linie des Polygonzuges
repräsentiert, hinzuaddiert wird, bis der Parameterbereich
verlassen wird.
- b.
- Berechne den Punkt
 xout
xout yout
yout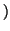 , an dem der
Polygonzug den Parameterbereich verläßt. Dazu suche zunächst
die letzte Linie im Polygonzug, bei der ein Punkt innerhalb und
ein Punkt außerhalb des Parameterbereiches liegt. Danach
überprüfe, welche der vier Randlinien einen Schnittpunkt mit
dieser Linie hat. Berechne den Schnittpunkt und setze lout
auf die Nummer der Linie (vgl. Abbildung 3.4).
, an dem der
Polygonzug den Parameterbereich verläßt. Dazu suche zunächst
die letzte Linie im Polygonzug, bei der ein Punkt innerhalb und
ein Punkt außerhalb des Parameterbereiches liegt. Danach
überprüfe, welche der vier Randlinien einen Schnittpunkt mit
dieser Linie hat. Berechne den Schnittpunkt und setze lout
auf die Nummer der Linie (vgl. Abbildung 3.4).
- c.
- Erzeuge den Eintrittspunkt
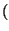 xin
xin 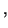 yin
yin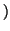 auf der Randlinie lin analog zu
auf der Randlinie lin analog zu
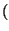 xout
xout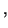 yout
yout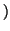 und lout.
und lout.
- d.
- Sind lin und lout gleich und
liegt
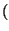 xin
xin 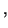 yin
yin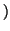 vor
vor
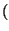 xout
xout 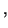 yout
yout auf dem
Rand, wenn dieser im Uhrzeigersinn durchlaufen wird, dann verbinde
beide Punkte. In diesem Fall ist der Polygonzug nun vollständig.
auf dem
Rand, wenn dieser im Uhrzeigersinn durchlaufen wird, dann verbinde
beide Punkte. In diesem Fall ist der Polygonzug nun vollständig.
- e.
- Sind lin und lout gleich und ist der
Umlaufsinn gegen den Uhrzeigersinn, dann verschiebe
lout um eine Linie im Uhrzeigersinn und füge den
übersprungenen Eckpunkt zum Polygonzug hinzu. Der Polygonzug
ist aber noch nicht vollständig, sondern muß im folgenden
Punkt erweitert werden.
- f.
- Solange lin nicht lout ist, verschiebe
lout um eine Linie im Uhrzeigersinn und füge
den übersprungenen Eckpunkt zum Polygonzug hinzu.
Nun fehlt noch der oben angesprochene Testalgorithmus für einen
Polygonzug. Diese Testfunktion muß überprüfen, ob ein vorgegebener
Punkt
 u
u v
v im Parameterbereich
durch die Trimmkurve ausgeschnitten wird. Die Trimmkurve ist dabei als
Polygonzug über die beiden Arrays x und y gegeben.
Der Umlaufsinn, mit dem
die Trimmkurve durchlaufen wird, gibt
normalerweise an, welcher Bereich innerhalb des Trimmbereiches liegt
und welcher außerhalb. Wir nehmen im folgenden immer an, daß der
Polygonzug im Uhrzeigersinn durchlaufen wird und alles, was rechts von
dem Polygonzug liegt, ausgeschnitten wird. Gebiete mit
entgegengesetztem Umlaufsinn können durch die Kombination mehrerer
Trimmkurven erzeugt werden. Wir werden dies weiter unten genauer
betrachten.
im Parameterbereich
durch die Trimmkurve ausgeschnitten wird. Die Trimmkurve ist dabei als
Polygonzug über die beiden Arrays x und y gegeben.
Der Umlaufsinn, mit dem
die Trimmkurve durchlaufen wird, gibt
normalerweise an, welcher Bereich innerhalb des Trimmbereiches liegt
und welcher außerhalb. Wir nehmen im folgenden immer an, daß der
Polygonzug im Uhrzeigersinn durchlaufen wird und alles, was rechts von
dem Polygonzug liegt, ausgeschnitten wird. Gebiete mit
entgegengesetztem Umlaufsinn können durch die Kombination mehrerer
Trimmkurven erzeugt werden. Wir werden dies weiter unten genauer
betrachten.
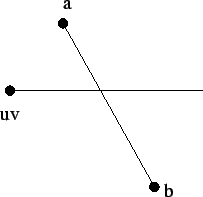
Abbildung 3.5:
Trimmkurventest
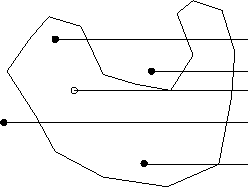 |
Zum Testen, ob ein Punkt im Trimmbereich liegt, zählen wir im
Algorithmus trimcurve_test, wie oft eine Linie von
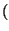 u
u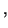 v
v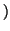 in Richtung
in Richtung 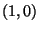 den
Polygonzug schneidet. Ist die Anzahl der Schnitte gerade, sind wir
außerhalb des Trimmbereiches, sonst innerhalb. Die Richtung ist dabei
beliebig. Ein paar Beispiele hierfür zeigt
Abbildung 3.5. Ist der Punkt innerhalb des
Trimmbereiches, muß die Linie wenigstens einmal den Rand schneiden.
Tritt die Linie an einer anderen Stelle wieder in den Trimmbereich
ein, dann muß sie diesen auch wieder verlassen, da er beschränkt ist.
Damit ist die Anzahl der Schnitte ungerade. Liegt der Punkt dagegen
außerhalb des Trimmbereichen, dann gibt es für jeden Eintrittspunkt in
den Trimmbereich auch wieder einen Austrittspunkt und so ist die
Anzahl der Schnitte gerade. Es gibt allerdings Fälle, wie für den
nicht ausgefüllten Punkt in Abbildung 3.5, bei
denen dieses Verfahren nicht funktioniert. Durch zusätzliche Tests,
etwa das Zählen der Schnitte mit Linien in andere Richtungen, lassen
sich solche Fälle weitere reduzieren, wir gehen hierauf aber nicht
näher ein. Für unsere Zwecke genügt die einfache Variante, wobei es
manchmal nötig sein kann die Auflösung der Testgitter und der
Trimmkurven anzupassen.
den
Polygonzug schneidet. Ist die Anzahl der Schnitte gerade, sind wir
außerhalb des Trimmbereiches, sonst innerhalb. Die Richtung ist dabei
beliebig. Ein paar Beispiele hierfür zeigt
Abbildung 3.5. Ist der Punkt innerhalb des
Trimmbereiches, muß die Linie wenigstens einmal den Rand schneiden.
Tritt die Linie an einer anderen Stelle wieder in den Trimmbereich
ein, dann muß sie diesen auch wieder verlassen, da er beschränkt ist.
Damit ist die Anzahl der Schnitte ungerade. Liegt der Punkt dagegen
außerhalb des Trimmbereichen, dann gibt es für jeden Eintrittspunkt in
den Trimmbereich auch wieder einen Austrittspunkt und so ist die
Anzahl der Schnitte gerade. Es gibt allerdings Fälle, wie für den
nicht ausgefüllten Punkt in Abbildung 3.5, bei
denen dieses Verfahren nicht funktioniert. Durch zusätzliche Tests,
etwa das Zählen der Schnitte mit Linien in andere Richtungen, lassen
sich solche Fälle weitere reduzieren, wir gehen hierauf aber nicht
näher ein. Für unsere Zwecke genügt die einfache Variante, wobei es
manchmal nötig sein kann die Auflösung der Testgitter und der
Trimmkurven anzupassen.
Wir beschreiben nun den Algorithmus zum Zeichnen getrimmter
G-Spline-Flächen. Die Umwandlung in Bézierkontrollnetze ändert
sich dabei nicht. Die impliziten Funktionen zum Trimmen im Raum der
Fläche geben wir allgemein für die Fläche an. Für die Trimmkurven
müssen wir dagegen auch das Bézierflächenstück festlegen. Nachdem
wir nur biquadratische Flächenstücke haben, genügt es für die
Trimmkurven einen G-Spline-Kontrollpunkt anzugeben. Dieser bestimmt
dann das Flächenstück. Im Algorithmus zeichnen wir jedes
Bézierflächenstück einzeln. Wir verwenden dazu die oben
vorgestellten
Abbildung 3.6:
Schnittbedingung (3.2)
 |
Testfunktionen. Zusätzlich müssen wir allerdings
berücksichtigen, daß mehrere Trimmkurven und implizite Funktionen für
ein Flächenstück angegeben werden können. Dabei gehen wir davon aus,
daß implizite Funktionen immer Teile aus der Fläche ausschneiden, auch
wenn die Volumina sich überlappen.
Bei Trimmkurven können sich dagegen auch “Inseln” bilden. Liegt ein
Punkt im Parameterbereich innerhalb einer geraden Anzahl von
Trimmbereichen, dann wird er nicht ausgeschnitten. Liegt er in einer
ungeraden Anzahl von Trimmbereichen wird er ausgeschnitten (vgl.
Abbildung 3.8). Damit entstehen keine Probleme, wenn
sich die Trimmkurven schneiden oder der Umlaufsinn der Trimmkurven
nicht zusammenpaßt. Eigentlich ignorieren wir den Umlaufsinn einfach.
Deshalb nehmen wir auch wie oben beschrieben immer an, daß die
Trimmkurven im Uhrzeigersinn durchlaufen werden. Trimmkurven, die
gegen den Uhrzeigersinn durchlaufen werden, lassen sich trotzdem
modellieren. Soll z.B. alles, was außerhalb eines Kreises im
Parameterbereich liegt, weggeschnitten werden, genügt es den Rand von
![[0,1]^2](img589.png) zusätzlich zum Kreis als Trimmkurve anzugeben.
zusätzlich zum Kreis als Trimmkurve anzugeben.
Algorithmus 3.3
| trimmed_bezier |
| Zeichnen eines getrimmten Bézierflächenstückes |
- 1.
- Lege über das Intervall
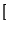 u0
u0 u1
u1![]x[](img587.png) v0
v0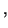 v1
v1![]](img719.png) ein Gitter mit
resolution
ein Gitter mit
resolution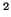 Punkten und prüfe, ob
die Gitterknoten innerhalb oder außerhalb der Trimmbereiche liegen:
Punkten und prüfe, ob
die Gitterknoten innerhalb oder außerhalb der Trimmbereiche liegen:
- (a)
- Initialisiere ein zwei-dimensionales boolean Array b0
für die
resolution
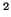 Gitterpunkte mit false.
Es wird true für ausgeschnittene und false für die
anderen Gitterpunkte sein.
Gitterpunkte mit false.
Es wird true für ausgeschnittene und false für die
anderen Gitterpunkte sein.
- (b)
- Prüfe für jeden Gitterpunkt mit den Koordinaten
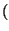 u
u v
v

 u0
u0  ui
ui 
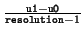
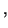 v0
v0  vi
vi 
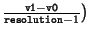 ,
wobei ui und vi die Position im b0 Array
festlegen und jeweils von 0 bis
resolution
,
wobei ui und vi die Position im b0 Array
festlegen und jeweils von 0 bis
resolution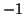 hochgezählt werden, ob sie in einem Trimmbereich liegen:
hochgezählt werden, ob sie in einem Trimmbereich liegen:
- i.
- Zähle die Anzahl der Trimmbereiche, die die Koordinaten
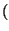 u
u v
v des Knotens enthalten, mit
Hilfe des Algorithmus' trimcurve_test. Die zu dem
Bézierflächenstück gehörenden Trimmkurven müssen vorher bekannt
sein.
des Knotens enthalten, mit
Hilfe des Algorithmus' trimcurve_test. Die zu dem
Bézierflächenstück gehörenden Trimmkurven müssen vorher bekannt
sein.
- ii.
- Ist die Anzahl ungerade, dann setze b0 für diesen
Gitterpunkt auf true.
- iii.
- Überprüfe, ob der zu
 u
u v
v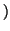 gehörende Punkt auf dem Bézierflächenstück wenigstens eine der
impliziten Trimmfunktionen erfüllt. Ist dies der Fall, setze
b0 für diesen Gitterpunkt auf true.
gehörende Punkt auf dem Bézierflächenstück wenigstens eine der
impliziten Trimmfunktionen erfüllt. Ist dies der Fall, setze
b0 für diesen Gitterpunkt auf true.
- 2.
- Bearbeite nun jedes Quadrat im Parameterbereich, das durch die
zwei Gitterknoten mit den Indizes [ui,vi] und
[ui+1,vi+1] bzgl. b0 bestimmt ist, um das
zugehörige Teil der Fläche zu zeichnen:
- (a)
- Wenn wenigstens eine der Ecken des Quadrats laut b0
in einem Trimmbereich liegt:
- i.
- Ist die maximale Rekursionstiefe für den Trimmalgorithmus
noch nicht erreicht, rufe trimmed_bezier rekursiv für
dieses Quadrat mit der um
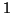 erhöhten Rekursionstiefe auf.
erhöhten Rekursionstiefe auf.
- ii.
- Sonst überprüfe, ob eines der durch die Ecken des Quadrats
bestimmten Dreiecke außerhalb des Trimmbereiches liegt und zeichne
das zugehörige Teil der Fläche als Dreieck.
- (b)
- Liegt keine der Ecken in einem Trimmbereich, dann zeichne den
zu diesem Quadrat gehörenden Teil der Fläche durch zwei Dreiecke.
Abbildung 3.7:
Getrimmtes Kreuz
|
|
trimmed_bezier wird mit einer Liste der Trimmkurven
aufgerufen, die zu dem jeweiligen Bézierflächenstück gehören. Diese
Liste kann über den zu jeder Trimmkurve angegebenen Kontrollpunkt der
Abbildung 3.8:
Überlappende Trimmbereiche
 |
G-Spline-Fläche bestimmt werden. Beim ersten Aufruf wählen wir
normalerweise das Einheitsquadrat als Parameterbereich und die
Rekursionstiefe ist 0. Das Trimming wird im Algorithmus vor allem
durch I. implementiert. Dieser Teil kann in ähnlicher
Form auch in den anderen Algorithmen für getrimmte Flächen verwendet
werden.
Bei trimmed_bezier ist zu berücksichtigen, daß die Auflösung
für das Testgitter groß genug gewählt wird. Ansonsten ist es möglich,
daß kleine Trimmbereiche ausgelassen werden. Auf der anderen Seite
sollte aber vor allem die maximale Rekursionstiefe klein sein, da
sonst der Algorithmus am Rand der Trimmbereiche sehr lange arbeitet.
Die maximale Rekursionstiefe sollte der benötigten Grafikauflösung für
die Darstellung angepaßt sein.
Die Trimmkurven können wir nicht für Flächen verwenden, auf die der
Doo-Sabin-Subdivision-Algorithmus angewendet wurde. In unserer
Implementierung des Doo-Sabin-Subdivision-Algorithmus' wird das
alte Kontrollnetz vollständig durch ein neues ersetzt. Da die
Trimmkurven an die alten Kontrollpunkte gebunden sind, verlieren wir
hierbei alle Trimmkurven. Wir gehen in dieser Arbeit nicht näher auf
dieses Problem ein, es wäre allerdings sinnvoll eine Übertragung der
Trimmkurven auf die neuen Kontrollpunkte zu entwickeln. In diesem
Zusammenhang sollte man auch eine Methode einführen, Trimmkurven über
mehrere Parameterbereiche anzugeben. Implizite Funktionen können
dagegen auch für Flächen zusammen mit der Doo-Sabin-Subdivision
verwendet werden.
Abbildung 3.7 zeigt das Kreuz aus Abbildung 1.23,
aus dem über eine implizite Funktion eine Kugel ausgeschnitten wurde.
In Abbildung 3.9 zeigen wir den Würfel aus
Abbildung 1.19, bei dem drei zu den Koordinatenachsen
parallele Zylinder ausgeschnitten wurden.
Abbildung 3.10 stellt eine G-Spline-Fläche mit
einer Irregularität der Ordnung 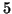 dar, bei der jeder Kontrollpunkt
an der Irregularität mit jeweils drei quadratischen, nicht
geschlossenen Trimmkurven und einem Trimmpolygon versehen wurde.
dar, bei der jeder Kontrollpunkt
an der Irregularität mit jeweils drei quadratischen, nicht
geschlossenen Trimmkurven und einem Trimmpolygon versehen wurde.
Abbildung 3.9:
Getrimmter Würfel
|
|
Abbildung 3.10:
Getrimmte G-Spline-Fläche mit einer Irregularität der Ordnung 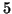
|
|



Next: 3.2 Funktionen auf getrimmten
Up: 3. Getrimmte Flächen
Previous: 3. Getrimmte Flächen
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node26.html
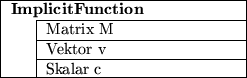
![]() . Die Trimmkurve
kann diesen Bereich aber verlassen.
. Die Trimmkurve
kann diesen Bereich aber verlassen.
![]() b[n-1]
in einen Polygonzug
b[n-1]
in einen Polygonzug
![]() x[0]
x[0]![]() y[0]
y[0]![]()
![]() x[N-1]
x[N-1]![]() y[N-1]
y[N-1]![]() um. Dabei ist zu beachten, daß wir aus den Kontrollpunkten zunächst
die Bézierpunkte für eine geometrisch glatte, quadratische Kurve
berechnen. Für jedes quadratische Segment der Trimmkurve benötigen wir
um. Dabei ist zu beachten, daß wir aus den Kontrollpunkten zunächst
die Bézierpunkte für eine geometrisch glatte, quadratische Kurve
berechnen. Für jedes quadratische Segment der Trimmkurve benötigen wir
![]() Linien, wenn step die
Schrittweite zur Berechnung der quadratischen Kurve ist. Wenn wir
die Kurve mit dem Rand von
Linien, wenn step die
Schrittweite zur Berechnung der quadratischen Kurve ist. Wenn wir
die Kurve mit dem Rand von ![]() erweitern müssen, kommen noch
maximal vier Ecken hinzu. Für die Punkte, an denen wir das
Einheitsquadrat für die Erweiterung verlassen und eintreten, haben
wir nochmal zwei zusätzliche Punkte für den Polygonzug. Insgesamt ist
erweitern müssen, kommen noch
maximal vier Ecken hinzu. Für die Punkte, an denen wir das
Einheitsquadrat für die Erweiterung verlassen und eintreten, haben
wir nochmal zwei zusätzliche Punkte für den Polygonzug. Insgesamt ist
![]() also nicht größer als
also nicht größer als
![]() .
.
![]() u
u![]() v
v![]() im Parameterbereich
durch die Trimmkurve ausgeschnitten wird. Die Trimmkurve ist dabei als
Polygonzug über die beiden Arrays x und y gegeben.
Der Umlaufsinn, mit dem
die Trimmkurve durchlaufen wird, gibt
normalerweise an, welcher Bereich innerhalb des Trimmbereiches liegt
und welcher außerhalb. Wir nehmen im folgenden immer an, daß der
Polygonzug im Uhrzeigersinn durchlaufen wird und alles, was rechts von
dem Polygonzug liegt, ausgeschnitten wird. Gebiete mit
entgegengesetztem Umlaufsinn können durch die Kombination mehrerer
Trimmkurven erzeugt werden. Wir werden dies weiter unten genauer
betrachten.
im Parameterbereich
durch die Trimmkurve ausgeschnitten wird. Die Trimmkurve ist dabei als
Polygonzug über die beiden Arrays x und y gegeben.
Der Umlaufsinn, mit dem
die Trimmkurve durchlaufen wird, gibt
normalerweise an, welcher Bereich innerhalb des Trimmbereiches liegt
und welcher außerhalb. Wir nehmen im folgenden immer an, daß der
Polygonzug im Uhrzeigersinn durchlaufen wird und alles, was rechts von
dem Polygonzug liegt, ausgeschnitten wird. Gebiete mit
entgegengesetztem Umlaufsinn können durch die Kombination mehrerer
Trimmkurven erzeugt werden. Wir werden dies weiter unten genauer
betrachten.
![]() zusätzlich zum Kreis als Trimmkurve anzugeben.
zusätzlich zum Kreis als Trimmkurve anzugeben.
![]() dar, bei der jeder Kontrollpunkt
an der Irregularität mit jeweils drei quadratischen, nicht
geschlossenen Trimmkurven und einem Trimmpolygon versehen wurde.
dar, bei der jeder Kontrollpunkt
an der Irregularität mit jeweils drei quadratischen, nicht
geschlossenen Trimmkurven und einem Trimmpolygon versehen wurde.

