Next: 1.4 Geometrische Stetigkeit Up: 1. Kurven und Flächen Previous: 1.2 Splineräume und B-Splines Inhalt

1.3 Bézierkurven

Wir betrachten nun eine Knotenfolge, in der jeder Knoten die maximale Vielfachheit besitzt. Es genügt ein einzelnes Intervall mit -fachen Randknoten zu untersuchen, z.B.

$u_{-d} = ... = u_0 < u_1 = ... = u_{1+d}.$

(1.10)

Dann lautet die Rekursionsformel für die für dieses Intervall relevanten B-Splines

$B_j^d(x) = (x - u_0)/(u_1 - u_0) B_j^{d-1}(x) + (u_1 - x)/(u_1 - u_0) B_{j+1}^{d-1}(x)$

(1.11)

mit $B_j^d := B_{j-d,d}$ . Über vollständige Induktion kann man dann beweisen, daß

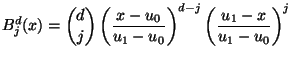$B_j^d(x) = \binom{d}{j} ((x - u_0)/(u_1 - u_0))^{d-j} ((u_1 - x)/(u_1 - u_0))^j$

(1.12)

gilt. Für das Intervall

erhält man so die Bernstein-Polynome.

Definition 1.3 (Bernstein-Polynome) Die Bernstein-Polynome

für

vom Grad

seien definiert durch

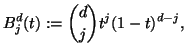$B^d_j(t) := \binom{d}{j} t^j(1-t)^{d-j},$

(1.13)

wobei die Binomialkoeffizienten durch

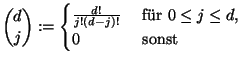$\binom{d}{j} := d!/(j!(d-j)!) für 0 <= j <= d, 0 sonst$

(1.14)

gegeben sind.

**Abbildung 1.4:** Quadratische Bernstein-Polynome

In Abbildung 1.4 sind die quadratischen Bernstein-Polynome dargestellt.

Es gilt

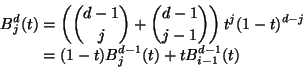$B^d_j(t) = (\binom{d-1}{j} + ... = (1-t)B^{d-1}_j(t) + tB^{d-1}_{i-1}(t)$

(1.15)

mit $B^0_0(t) \equiv 1$ und $B^d_j(t) \equiv 0$ für $j \notin {0, 1, ..., d}$ . Hieraus erhält man eine einfache Methode, um Bernstein-Polynome von Grad

aus denen von Grad

zu berechnen. Weiterhin folgt aus dem binomischen Satz, daß

$\sum_{j=0}^d B_j^d(t) = \sum_{j=0}^d \binom{d}{j} t^j (1-t)^{d-j} = (t+(1-t))^d = 1.$

(1.16)

Die Ableitung eines Bernstein-Polynoms berechnet sich nach der Rekursionsformel

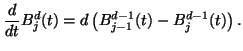$d/dt B^d_j(t) = d (B^{d-1}_{j-1}(t) - B^{d-1}_j(t)).$

(1.17)

Mit Hilfe der Bernstein-Polynome lassen sich nun die Bézierkurven definieren.

Definition 1.4 (Bézierkurven) Eine Bézierkurve vom Grad

mit den Kontrollpunkten (Bézierpunkten) $p_j \in R^N$ ,

sei definiert durch

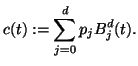$c(t) := \sum_{j=0}^d p_j B^d_j(t).$

(1.18)

**Abbildung 1.5:** Bézierkurve

Jede Splinekurve (1.9) läßt sich durch Bézierkurven darstellen, indem man in die gegebene Knotenfolge

jeden Knoten solange einfügt bis er die Vielfachheit

hat (siehe [Höl94]). Die Splinekurve wird dann aus Bézierkurven vom Grad

mit jeweils

Kontrollpunkten zusammengesetzt. Bézierkurven sind damit spezielle Splinekurven mit sehr nützlichen Eigenschaften. Man erkennt dies schon an Abbildung 1.5, welche eine Bézierkurve vom Grad

zeigt.

Wegen (1.16) und folgt direkt aus der Definition, daß Bézierkurven immer in der konvexen Hülle ihrer Kontrollpunkte liegen. Aus den beiden Eigenschaften folgt auch, daß Bézierkurven affin invariant sind, da baryzentrische Kombinationen invariant unter affinen Abbildungen sind, d.h. wenn man eine affine Abbildung auf die Kurve anwendet, erzeugt dies die gleiche Kurve, wie wenn man die affine Abbildung auf die Kontrollpunkte anwendet. Eine Bézierkurve ist auch invariant unter einer affinen Parametertransformation $T: [0,1] \to [a,b], t -> t'$ , d.h. es gilt

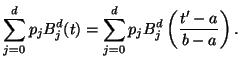$\sum_{j=0}^d p_j B_j^d(t) = \sum_{j=0}^d p_j B^d_j ((t'-a)/(b-a)).$

(1.19)

Weiter erhält man sofort aus der Definition der Bernstein-Polynome, daß

$B^d_j(t) = B^d_{d-j}(1-t).$

(1.20)

Damit gilt

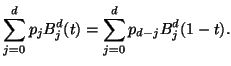$\sum_{j=0}^d p_j B^d_j(t) = \sum_{j=0}^d p_{d-j}B^d_j(1-t).$

(1.21)

Dies bedeutet, daß die Kontrollpunkte sowohl mit

, als auch mit

bezeichnet werden können.

Es gilt auch und , da $B^d_j(0) = delta_{j,0}$ und $B^d_j(1) = delta_{j,d}$ wobei $delta_{j,d}$ das Kroneckersymbol bezeichnet. Damit interpolieren die Bézierkurven immer den Anfangs- und Endpunkt des Kontrollpolygons. Weiter gilt auch, daß die Richtung der Tangente der Kurve in und der Richtung der ersten Strecke des Kontrollpolygons von nach bzw. der letzten Strecke von $p_{d-1}$ nach entspricht.

Man kann weiter zeigen, daß gilt

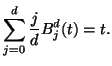$\sum_{j=0}^d j/d B^d_j(t) = t.$

(1.22)

Wenn man also die Kontrollpunkte gleichmäßig auf einer Geraden, die die Punkte

und

verbindet, verteilt, d.h.

, dann erzeugt

genau die Strecke von

nach

. Diese Eigenschaft heißt lineare Präzision.

Das Bernstein-Polynom besitzt nur ein Maximum an der Stelle , d.h. wenn wir nur einen Kontrollpunkt ändern, ist die Änderung der Kurve im Bereich des Parameterwertes am stärksten. Dadurch werden die Auswirkungen von Änderungen vorhersehbar und vor allem ändert sich der Verlauf der Kurve nur in einem lokal beschränkten Bereich.

Next: 1.4 Geometrische Stetigkeit Up: 1. Kurven und Flächen Previous: 1.2 Splineräume und B-Splines Inhalt

Copyright © 1999-2002 Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.1 or any later version published by the Free Software Foundation.

Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node9.html