 |
Nach dem Approximationssatz für stetige Funktionen von Weierstraß
lassen sich stetige Funktionen auf einem endlichen, abgeschlossenen
Intervall beliebig genau durch Polynome approximieren. In der
Anwendung könnte man also eine solche Funktion
![]() (
(
![]() ) durch ein Polynom darstellen.
) durch ein Polynom darstellen.
Eine Möglichkeit hierfür wäre die diskrete Approximation bzw.
Interpolation. Dazu wählt man ![]() Stützstellen
Stützstellen
![]() zu den Stützwerten
zu den Stützwerten
![]() und
fordert, daß das Interpolationspolynom
und
fordert, daß das Interpolationspolynom
![]() die
Stützwerte an den Stützstellen annimmt, also
die
Stützwerte an den Stützstellen annimmt, also
![]() für
für
![]() . Dann ist
. Dann ist ![]() eindeutig durch die Lagrange'sche
Interpolationsformel bestimmt,
eindeutig durch die Lagrange'sche
Interpolationsformel bestimmt,
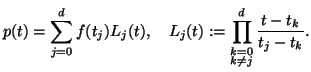 |
(1.1) |
Allerdings ergeben sich bei dieser Methode auch einige Probleme. Jedes
![]() ist von allen Stützstellen abhängig, d.h.
ist von allen Stützstellen abhängig, d.h. ![]() hängt global von
den Stützstellen ab und muß bei jeder Änderung einzelner
Approximationsdaten vollständig neu berechnet werden.
hängt global von
den Stützstellen ab und muß bei jeder Änderung einzelner
Approximationsdaten vollständig neu berechnet werden.
Ist der Funktionswert einer Polynomfunktion an einer Stelle von 0 verschieden und nicht konstant, dann strebt die Funktion für große
Weiterhin erhöht sich der Grad von ![]() um eins für jede weitere
Stützstelle, womit auch die Berechnung des Polynoms selbst sehr
komplex werden kann. Ein Polynom von hohem Grad approximiert den
Gesamtverlauf der Funktion auch nicht unbedingt zufriedenstellend.
Siehe hierzu auch Abbildung 1.2, in der die
Funktion
um eins für jede weitere
Stützstelle, womit auch die Berechnung des Polynoms selbst sehr
komplex werden kann. Ein Polynom von hohem Grad approximiert den
Gesamtverlauf der Funktion auch nicht unbedingt zufriedenstellend.
Siehe hierzu auch Abbildung 1.2, in der die
Funktion
![]() an den Stellen
an den Stellen
![]() interpoliert wurde (vgl. [Höl98]). Die Orginalfunktion ist
gepunktet eingezeichnet.
interpoliert wurde (vgl. [Höl98]). Die Orginalfunktion ist
gepunktet eingezeichnet.