


Next: 1.3 Bézierkurven
Up: 1. Kurven und Flächen
Previous: 1.1 Approximation mit Polynomen
Inhalt
Polynome sind dagegen sehr gut zur lokalen Approximation von glatten
Funktionen geeignet. Um die Probleme der polynomialen Interpolation zu
vermeiden, liegt es daher nahe, die Funktion stückweise durch Polynome
zu approximieren. Dazu teilen wir ein Interval
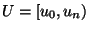 in
in 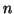 Teilintervalle
Teilintervalle
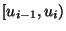 ,
, 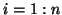 auf, die durch die
Knotenfolge
auf, die durch die
Knotenfolge
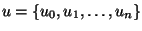 mit
mit
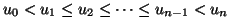 |
(1.2) |
bestimmt werden. Auf jedem dieser Teilintervalle stellen wir die
approximierende Funktion 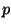 als Polynom vom maximalen Grad
als Polynom vom maximalen Grad 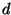 dar.
Dabei kann in der Knotenfolge jeder Knoten maximal
dar.
Dabei kann in der Knotenfolge jeder Knoten maximal 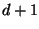 -mal
vorkommen. Kommt ein Knoten
-mal
vorkommen. Kommt ein Knoten 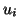 genau
genau 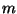 -mal vor, d.h.
-mal vor, d.h.
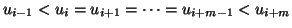 , dann sind die ersten
, dann sind die ersten
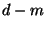 Ableitungen von
Ableitungen von 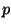 an diesem Knoten stetig.
an diesem Knoten stetig. 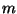 heißt die
Vielfachheit von
heißt die
Vielfachheit von 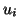 .
. 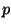 ist dann eine Splinefunktion zur
Knotenfolge
ist dann eine Splinefunktion zur
Knotenfolge 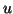 vom Grad
vom Grad 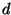 mit dem Definitionsbereich
mit dem Definitionsbereich 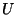 . Den
hieraus entstehenden Splineraum bezeichnen wir mit
. Den
hieraus entstehenden Splineraum bezeichnen wir mit
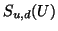 . Um
eine Basis für diesen Raum zu erhalten, erweitern wir zunächst die
Knotenfolge
. Um
eine Basis für diesen Raum zu erhalten, erweitern wir zunächst die
Knotenfolge 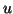 in beide Richtungen um jeweils
in beide Richtungen um jeweils 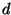 Punkte:
Punkte:
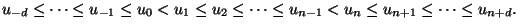 |
(1.3) |
Wir können auch annehmen, daß 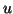 in beide Richtungen unendlich
fortgesetzt wird und wir nur die jeweils relevanten Knoten betrachten.
Die Knoten außerhalb des Intervalls
in beide Richtungen unendlich
fortgesetzt wird und wir nur die jeweils relevanten Knoten betrachten.
Die Knoten außerhalb des Intervalls 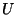 haben keinen Einfluß auf die
im Splineraum enthaltenen Funktionen. Eine mögliche Basis für diesen
Raum bilden die abgebrochenen Potenzen. Jedes
haben keinen Einfluß auf die
im Splineraum enthaltenen Funktionen. Eine mögliche Basis für diesen
Raum bilden die abgebrochenen Potenzen. Jedes
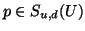 läßt sich darstellen als
läßt sich darstellen als
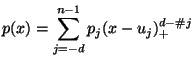 |
(1.4) |
mit den Koeffizienten
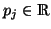 und
und
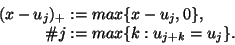 |
(1.5) |
Dabei ergeben die ersten 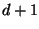 abgebrochenen Potenzen eine Basis für
die Polynome vom maximalen Grad
abgebrochenen Potenzen eine Basis für
die Polynome vom maximalen Grad 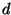 auf dem Intervall
auf dem Intervall
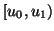 .
Die restlichen Terme bestimmen die “Sprünge” in den Ableitungen an
den Knoten. Aus dieser Darstellung folgt, daß die Dimension von
.
Die restlichen Terme bestimmen die “Sprünge” in den Ableitungen an
den Knoten. Aus dieser Darstellung folgt, daß die Dimension von
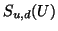 gleich
gleich 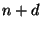 ist.
ist.
Die Basis der abgebrochenen Potenzen (1.4)
für
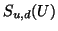 besitzt allerdings keinen kompakten Support, d.h.
Änderungen der Koeffizienten
besitzt allerdings keinen kompakten Support, d.h.
Änderungen der Koeffizienten  haben globale Auswirkungen. Dieser
Nachteil wird durch die B-Splines aufgehoben.
haben globale Auswirkungen. Dieser
Nachteil wird durch die B-Splines aufgehoben.
Definition 1.1 (B-Splines)
Zu einer vorgegebenen Knotenfolge
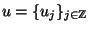
für die
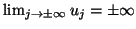
gilt, sei der B-Spline
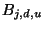
vom Grad
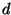
wie folgt rekursiv definiert.
Für

sei
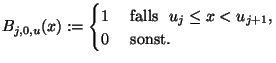 |
(1.6) |
Für
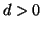
sei
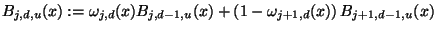 |
(1.7) |
mit
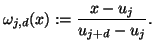 |
(1.8) |
Abbildung 1.3:
Rekursive Definition eines B-Splines vom Grad 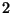
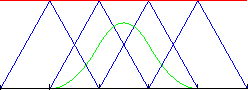 |
Die rekursive Konstruktion eines B-Splines vom Grad 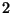 für eine
äquidistante Knotenfolge ist in Abbildung 1.3
veranschaulicht. Mit Hilfe der Marsden Identität erhält man folgendes
Resultat.
für eine
äquidistante Knotenfolge ist in Abbildung 1.3
veranschaulicht. Mit Hilfe der Marsden Identität erhält man folgendes
Resultat.
Theorem 1.2 (B-Spline Basis)
Für das Intervall
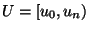
bilden die B-Splines
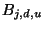
für
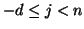
eine Basis für
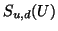
mit der Knotenfolge
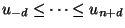
und es gilt
![supp(B_{j,d,u}) = [u_j,u_{j+d+1}]](img62.png)
. Falls
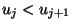
,
bilden die B-Splines
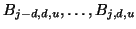
eine Basis der Polynome vom maximalen
Grad
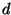
auf
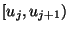
.
Proof.
Den Beweis hierzu findet man in [
Höl94] und [
Höl98].
Eine Splinekurve 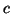 vom Grad
vom Grad 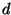 im
im
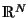 mit den Kontrollpunkten
mit den Kontrollpunkten
![p_j = [p_{j,1}, ..., p_{j,D}]^T \in R^N](img68.png) hat demnach die Form
hat demnach die Form
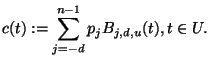 |
(1.9) |
Damit sind die Koordinatenfunktionen von 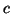 Splinefunktionen aus
Splinefunktionen aus
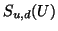 .
.



Next: 1.3 Bézierkurven
Up: 1. Kurven und Flächen
Previous: 1.1 Approximation mit Polynomen
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node8.html
![]() in
in ![]() Teilintervalle
Teilintervalle
![]() ,
, ![]() auf, die durch die
Knotenfolge
auf, die durch die
Knotenfolge
![]() mit
mit
![]() besitzt allerdings keinen kompakten Support, d.h.
Änderungen der Koeffizienten
besitzt allerdings keinen kompakten Support, d.h.
Änderungen der Koeffizienten ![]() haben globale Auswirkungen. Dieser
Nachteil wird durch die B-Splines aufgehoben.
haben globale Auswirkungen. Dieser
Nachteil wird durch die B-Splines aufgehoben.
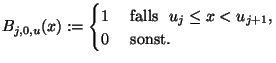
![]() für eine
äquidistante Knotenfolge ist in Abbildung 1.3
veranschaulicht. Mit Hilfe der Marsden Identität erhält man folgendes
Resultat.
für eine
äquidistante Knotenfolge ist in Abbildung 1.3
veranschaulicht. Mit Hilfe der Marsden Identität erhält man folgendes
Resultat.
![]() vom Grad
vom Grad ![]() im
im
![]() mit den Kontrollpunkten
mit den Kontrollpunkten
![]() hat demnach die Form
hat demnach die Form