


Next: 1.6 Geometrisch glatte Flächen
Up: 1. Kurven und Flächen
Previous: 1.4 Geometrische Stetigkeit
Inhalt
Abbildung 1.7:
Tensorproduktfläche
 |
Nun sollen mit Hilfe der Splinefunktionen, insbesondere der
Bézierkurven, Flächen im
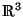 dargestellt werden.
Intuitiv kann man eine Fläche auch als Kurve auffassen, die sich durch
den Raum bewegt und dabei ihre Form verändert (vgl. [Far93]).
Dies ist schematisch in Abbildung 1.7 dargestellt.
Wir beschränken uns im folgenden darauf, daß diese Kurve zu
jedem Zeitpunkt eine Bézierkurve vom Grad
dargestellt werden.
Intuitiv kann man eine Fläche auch als Kurve auffassen, die sich durch
den Raum bewegt und dabei ihre Form verändert (vgl. [Far93]).
Dies ist schematisch in Abbildung 1.7 dargestellt.
Wir beschränken uns im folgenden darauf, daß diese Kurve zu
jedem Zeitpunkt eine Bézierkurve vom Grad 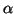 ist. Sei
ist. Sei 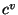 die Kurve zum Zeitpunkt
die Kurve zum Zeitpunkt 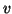 , wobei
, wobei 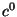 die Anfangskurve und
die Anfangskurve und 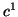 die Endkurve sei,
die Endkurve sei,
![c^v: [0,1] -> R^3, u -> \sum_{j=0}^alpha P_j(v)B^alpha_j(u).](img147.png) |
(1.27) |
Bewegt sich diese Kurve im Raum, so wird ihre Form zu jedem Zeitpunkt
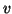 durch eine Menge von Kontrollpunkten
durch eine Menge von Kontrollpunkten
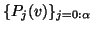 bestimmt. Damit geht von jedem einzelnen ursprünglichen Kontrollpunkt
bestimmt. Damit geht von jedem einzelnen ursprünglichen Kontrollpunkt
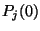 eine Kurve aus, die die Lage der folgenden Kontrollpunkte
beschreibt. Wir beschränken uns nun weiter darauf, daß auch diese
Kurven Bézierkurven vom festen Grad
eine Kurve aus, die die Lage der folgenden Kontrollpunkte
beschreibt. Wir beschränken uns nun weiter darauf, daß auch diese
Kurven Bézierkurven vom festen Grad 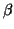 sind, die selbst durch
Kontrollpunkte beschrieben werden, d.h.
sind, die selbst durch
Kontrollpunkte beschrieben werden, d.h. 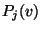 wird beschrieben
durch
wird beschrieben
durch
![P_j: [0,1] -> R^3, v -> \sum_{k=0}^beta P_{j,k} B^beta_k(v).](img152.png) |
(1.28) |
Kombiniert man beide Gleichungen, erhält man eine Fläche 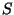 als
Tensorprodukt
als
Tensorprodukt
![S: [0,1]^2 -> R^3, (u,v) -> \sum_{j=0}^alpha \sum_{k=0}^beta P_{j,k} B^alpha_j(u) B^beta_k(v),](img154.png) |
(1.29) |
die durch die Punkte 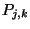 vollständig beschrieben wird. Viele der
Eigenschaften dieser Bézierflächen lassen sich direkt aus den
Eigenschaften der Bézierkurven ableiten (siehe auch [Far93]).
vollständig beschrieben wird. Viele der
Eigenschaften dieser Bézierflächen lassen sich direkt aus den
Eigenschaften der Bézierkurven ableiten (siehe auch [Far93]).
Die Originalkurve 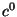 hat die Kontrollpunkte
hat die Kontrollpunkte
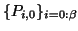 und es ist einfach zu zeigen, daß jede
beliebige Randkurve von
und es ist einfach zu zeigen, daß jede
beliebige Randkurve von 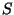 als Anfangskurve zu verwenden ist. Die
Randkurven der Fläche sind Polynomkurven und werden durch die
Randpunkte des Kontrollnetzes
als Anfangskurve zu verwenden ist. Die
Randkurven der Fläche sind Polynomkurven und werden durch die
Randpunkte des Kontrollnetzes 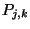 festgelegt. Insbesondere
liegen alle vier Ecken des Kontrollnetzes auf der Fläche.
festgelegt. Insbesondere
liegen alle vier Ecken des Kontrollnetzes auf der Fläche.
Es gilt
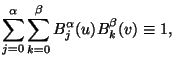 |
(1.30) |
d.h. (1.29) ist eine affine Kombination und somit affin
invariant.
Für
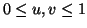 sind
sind
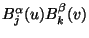 nicht negativ.
Zusammen mit (1.30) folgt damit, daß (1.29)
eine Konvexkombination ist. Die Fläche liegt somit in der konvexen
Hülle der Kontrollpunkte.
nicht negativ.
Zusammen mit (1.30) folgt damit, daß (1.29)
eine Konvexkombination ist. Die Fläche liegt somit in der konvexen
Hülle der Kontrollpunkte.



Next: 1.6 Geometrisch glatte Flächen
Up: 1. Kurven und Flächen
Previous: 1.4 Geometrische Stetigkeit
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node11.html

![c^v: [0,1] -> R^3, u -> \sum_{j=0}^alpha P_j(v)B^alpha_j(u).](img147.png)
![P_j: [0,1] -> R^3, v -> \sum_{k=0}^beta P_{j,k} B^beta_k(v).](img152.png)
![]() als
Tensorprodukt
als
Tensorprodukt
![]() hat die Kontrollpunkte
hat die Kontrollpunkte
![]() und es ist einfach zu zeigen, daß jede
beliebige Randkurve von
und es ist einfach zu zeigen, daß jede
beliebige Randkurve von ![]() als Anfangskurve zu verwenden ist. Die
Randkurven der Fläche sind Polynomkurven und werden durch die
Randpunkte des Kontrollnetzes
als Anfangskurve zu verwenden ist. Die
Randkurven der Fläche sind Polynomkurven und werden durch die
Randpunkte des Kontrollnetzes ![]() festgelegt. Insbesondere
liegen alle vier Ecken des Kontrollnetzes auf der Fläche.
festgelegt. Insbesondere
liegen alle vier Ecken des Kontrollnetzes auf der Fläche.
![]() sind
sind
![]() nicht negativ.
Zusammen mit (1.30) folgt damit, daß (1.29)
eine Konvexkombination ist. Die Fläche liegt somit in der konvexen
Hülle der Kontrollpunkte.
nicht negativ.
Zusammen mit (1.30) folgt damit, daß (1.29)
eine Konvexkombination ist. Die Fläche liegt somit in der konvexen
Hülle der Kontrollpunkte.