Durch die Knotenfolge (1.3) wird die Glattheit der
aus Polynomen zusammengesetzten Kurve festgelegt. Kommt ein Knoten
genau 
-mal vor, so sind die ersten 
Ableitungen der Kurve an
dieser Stelle stetig. Anstatt die Glattheit der Parametrisierung zu
fordern, können wir auch verlangen, daß die Kurve geometrisch glatt
ist.
![c: [u_0,u_n] -> R^N](img117.png){kind=small}
eine reguläre Parametrisierung einer
Splinekurve. Die Splinekurve ist eine -mal stetig
differenzierbare Kurve, wenn für jeden Knoten 
aus der
Knotenfolge (1.3) eine stetige Funktion 
mit
und 
existiert, so daß für
gilt
 |
(1.23) |
Für eine stetig differenzierbare Kurve erhalten wir damit die Bedingungen
. Dabei bedeutet die erste Gleichung nur, daß
die Kurve am Knoten zusammenhängt. Die zweite Gleichung
bedeutet, daß die Tangentenvektoren 
und 
in parallel,
aber nicht notwendig gleich sind.
Wir untersuchen dies nun speziell für Bézierkurven. Dazu können wir
die einzelnen als Bézierkurve darstellbaren Kurvensegmente zunächst
unabhängig voneinander betrachten. Jedes dieser Segmente wird durch
Kontrollpunkte bestimmt. Soll die gesamte Kurve einmal stetig
differenzierbar sein, dann müssen obige Gleichungen jeweils an den
Stellen gelten, an denen die Kurvensegmente zusammengesetzt werden.
Seien
und
die Kontrollpunkte
zweier benachbarter Kurvensegmente (vgl. Abbildung 1.6). Wir nehmen an,
daß (1.24) an 
erfüllt ist. Also gilt 
,
da Bézierkurven die Anfangs- und Endpunkte des Kontrollpolygons
interpolieren. Nach (1.25) müssen die Tangenten an parallel sein, d.h. Die Punkte 
, , und 
müssen kolinear sein, denn die Tangenten an den Anfangs- und
Endpunkten der Bézierkurven werden ebenfalls durch das
Kontrollpolygon bestimmt.
Falls eine Kurve eine glatte, reguläre Parametrisierung 
hat,
dann ist auch die Parametrisierung nach der Bogenlänge
 |
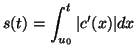(1.26) |
