


Next: 1.8 Algorithmen für biquadratische
Up: 1. Kurven und Flächen
Previous: 1.6 Geometrisch glatte Flächen
Inhalt
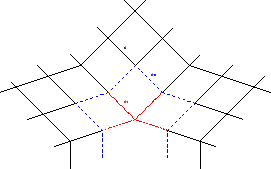
Abbildung 1.9:
Glattheitsbedingungen in der Nähe einer Irregularität
 |
Im vorherigen Abschnitt haben wir bereits eine Methode angesprochen,
mit der man aus einem regulären Kontrollnetz Bézierkontrollnetze
erzeugen kann, so daß die Fläche geometrisch glatt ist. Diese Methode
läßt sich auf semi-reguläre Netze erweitern. Hieraus werden wir die
biquadratischen G-Spline-Flächen erhalten. Die durch das
Kontrollnetz repräsentierte Fläche soll durch eine Anzahl
biquadratischer Bézierflächen dargestellt werden, d.h. zu jedem
Punkt des Kontrollnetzes wird eine Bézierfläche mit neun
Bézierpunkten erzeugt. Am Rand sollen diese Flächenstücke
geometrisch glatt zusammengesetzt werden. Im regulären Fall können wir
hierfür die Glattheitsbedingung von Typ 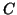 verwenden. In der Umgebung
einer Irregularität der Ordnung
verwenden. In der Umgebung
einer Irregularität der Ordnung 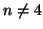 ist dies jedoch nicht
möglich, nachdem hier mehr oder weniger als vier Flächenstücke
zusammentreffen. An der Irregularität enthält das Kontrollnetz ein
Polygon mit mehr oder weniger als vier Kanten. Dem Ansatz von
[Rei95] folgend fordern wir in der Umgebung der Irregularität,
daß die Glattheitsbedingungen vom Typ
ist dies jedoch nicht
möglich, nachdem hier mehr oder weniger als vier Flächenstücke
zusammentreffen. An der Irregularität enthält das Kontrollnetz ein
Polygon mit mehr oder weniger als vier Kanten. Dem Ansatz von
[Rei95] folgend fordern wir in der Umgebung der Irregularität,
daß die Glattheitsbedingungen vom Typ 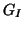 oder
oder 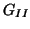 erfüllt
sind, wie in Abbildung 1.9 gezeigt. Dabei
stellen gepunktete Linien den Typ
erfüllt
sind, wie in Abbildung 1.9 gezeigt. Dabei
stellen gepunktete Linien den Typ 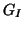 , gestrichelte den Typ
, gestrichelte den Typ 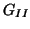 und der Rest den Typ
und der Rest den Typ 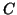 dar.
dar.
Abbildung 1.10:
Bezeichnungen der Bézierpunkte in der Nähe einer Irregularität
|
|
In der Umgebung der Irregularität bezeichnen wir die Bézierpunkte
wie in Abbildung 1.10 angegeben. Der Index
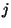 läuft dabei von 0 bis
läuft dabei von 0 bis 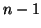 und wird modulo
und wird modulo 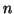 hochgezählt.
Wir fassen die Punkte vom gleichen Typ zu Vektoren zusammen, also
hochgezählt.
Wir fassen die Punkte vom gleichen Typ zu Vektoren zusammen, also
![A = [A_0, A_1, ..., A_{n-1}]](img251.png) , ...etc. Nach [Rei95] lassen sich
aus den Kontrollpunkten
, ...etc. Nach [Rei95] lassen sich
aus den Kontrollpunkten 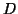 ,
, 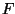 ,
, 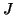 und
und 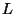 die Bézierkontrollnetze
berechnen, wenn diese bestimmten Gleichungen genügen.
die Bézierkontrollnetze
berechnen, wenn diese bestimmten Gleichungen genügen.
Theorem 1.8
Wenn die Kontrollpunkte die Gleichungen
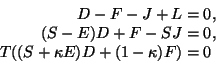 |
(1.43) |
mit dem Shift Operator
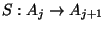
und der
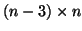
Matrix
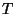
gegeben durch
erfüllen, dann beschreiben die durch folgende Gleichungen gegebenen
Bézierpunkte eine glatte, biquadratische Splinefläche:
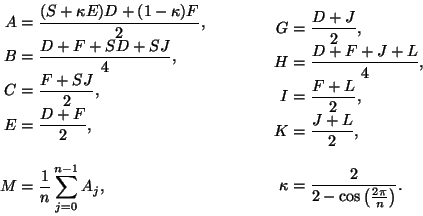 |
(1.45) |
Proof.
Der Beweis ist in [
Rei95] zu finden.
Abbildung 1.11:
G-Spline-Fläche mit Irregularität der Ordnung 3
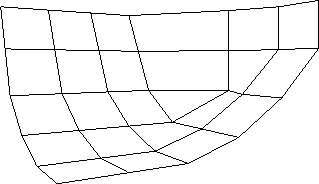
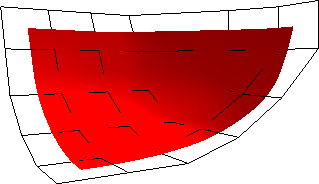 |
Abbildung 1.12:
G-Spline-Fläche mit Irregularität der Ordnung 5
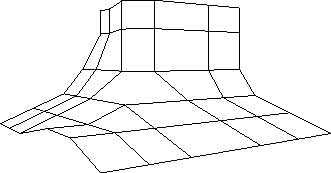
 |
Also lassen sich alle Punkte in Abhängigkeit von 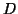 ,
, 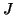 ,
, 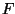 und
und 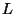 darstellen. Wir bezeichnen die
darstellen. Wir bezeichnen die 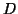 ,
, 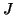 ,
, 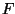 und
und 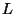 als
Quasikontrollpunkte, da diese Punkte immer noch die
Bedingungen (1.43) erfüllen müssen. Unser Ziel ist es auch diese
Bedingungen zu eliminieren. In Matrixform lauten sie
als
Quasikontrollpunkte, da diese Punkte immer noch die
Bedingungen (1.43) erfüllen müssen. Unser Ziel ist es auch diese
Bedingungen zu eliminieren. In Matrixform lauten sie
![[E, -E, -E, E; S-E, E, -S, 0; TS+kappa, T, ... T, 0, 0] = [D; F; J; L;] =: PX = 0,](img269.png) |
(1.46) |
wobei 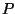 eine
eine
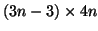 Matrix ist. Haben wir nun einen
Vektor
Matrix ist. Haben wir nun einen
Vektor
![x = [d;f;j;l]](img271.png) von beliebigen Kontrollpunkten, die eine Fläche
beschreiben sollen, dann kann ein passender Vektor
von beliebigen Kontrollpunkten, die eine Fläche
beschreiben sollen, dann kann ein passender Vektor 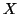 durch das
Optimierungsproblem
durch das
Optimierungsproblem
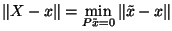 |
(1.47) |
gefunden werden (mit
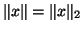 ). Die Lösung für dieses Problem
liefert die Pseudoinverse
). Die Lösung für dieses Problem
liefert die Pseudoinverse 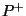 von
von 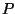 ,
,
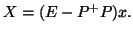 |
(1.48) |
Damit lassen sich also alle Bézierpunkte in der Umgebung der
Irregularität mit der Gleichung (1.48) und dem
Theorem 1.8 aus beliebigen Kontrollpunkten
berechnen. Die Abbildungen 1.11
und 1.12 zeigen das Kontrollnetz und die berechnete
G-Spline-Fläche für Kontrollnetze mit einer Irregularität der Ordnung 3 und 5.



Next: 1.8 Algorithmen für biquadratische
Up: 1. Kurven und Flächen
Previous: 1.6 Geometrisch glatte Flächen
Inhalt
Copyright © 1999-2002
Frank C. Langbein. All rights reserved.
Permission is granted to copy, distribute and/or modify this
document under the terms of the
GNU Free Documentation License, Version 1.1
or any later version published by the Free Software Foundation.
Contact: webmaster@langbein.org
URI: http://www.langbein.org/fileadmin/research/surfaces/diploma/HTML/node13.html

![]() läuft dabei von 0 bis
läuft dabei von 0 bis ![]() und wird modulo
und wird modulo ![]() hochgezählt.
Wir fassen die Punkte vom gleichen Typ zu Vektoren zusammen, also
hochgezählt.
Wir fassen die Punkte vom gleichen Typ zu Vektoren zusammen, also
![]() , ...etc. Nach [Rei95] lassen sich
aus den Kontrollpunkten
, ...etc. Nach [Rei95] lassen sich
aus den Kontrollpunkten ![]() ,
, ![]() ,
, ![]() und
und ![]() die Bézierkontrollnetze
berechnen, wenn diese bestimmten Gleichungen genügen.
die Bézierkontrollnetze
berechnen, wenn diese bestimmten Gleichungen genügen.
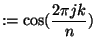 für
für 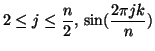 für
für ![]() ,
, ![]() ,
, ![]() und
und ![]() darstellen. Wir bezeichnen die
darstellen. Wir bezeichnen die ![]() ,
, ![]() ,
, ![]() und
und ![]() als
Quasikontrollpunkte, da diese Punkte immer noch die
Bedingungen (1.43) erfüllen müssen. Unser Ziel ist es auch diese
Bedingungen zu eliminieren. In Matrixform lauten sie
als
Quasikontrollpunkte, da diese Punkte immer noch die
Bedingungen (1.43) erfüllen müssen. Unser Ziel ist es auch diese
Bedingungen zu eliminieren. In Matrixform lauten sie
![[E, -E, -E, E; S-E, E, -S, 0; TS+kappa, T, ... T, 0, 0] = [D; F; J; L;] =: PX = 0,](img269.png)