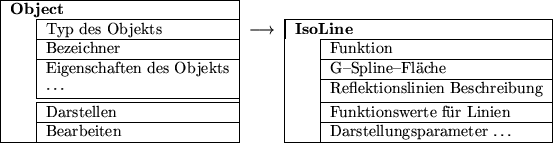 |
Neben der Darstellung durch Farben bzw. als Gitter oder Fläche über der Fläche können wir G-Spline-Funktionen auch durch Isolinien oder Niveaulinien darstellen. Dazu zeichnen wir auf der Fläche eine Linie, entlang der die Funktion den gleichen Wert hat. Die Werte, für die wir solche Linien zeichnen, können entweder äquidistant sein, oder wir können eine Liste spezieller Werte angeben.
Im Prinzip ist der Algorithmus für diese Darstellung ein
verallgemeinerter Plotter für Contourlinien einer Funktion
![]() . Für die Isolinien leiten wir von Object eine neue
Klasse IsoLine ab, die Zeiger auf die Fläche und die Funktion
besitzt und die Darstellung der Isolinien genauer beschreibt, wie in
Abbildung 2.13 dargestellt. Wir gehen davon aus, daß
die Fläche und die Funktion bereits durch biquadratische
Bézierkontrollnetze beschrieben werden. Wieder bearbeiten wir jedes
Bézierkontrollnetz einzeln. Der Algorithmus isolines
zeichnet die Isolinien für das Bézierkontrollnetz fb der
Funktion, auf der durch das Bézierkontrollnetz b gegebenen
Fläche, für den Parameterbereich
. Für die Isolinien leiten wir von Object eine neue
Klasse IsoLine ab, die Zeiger auf die Fläche und die Funktion
besitzt und die Darstellung der Isolinien genauer beschreibt, wie in
Abbildung 2.13 dargestellt. Wir gehen davon aus, daß
die Fläche und die Funktion bereits durch biquadratische
Bézierkontrollnetze beschrieben werden. Wieder bearbeiten wir jedes
Bézierkontrollnetz einzeln. Der Algorithmus isolines
zeichnet die Isolinien für das Bézierkontrollnetz fb der
Funktion, auf der durch das Bézierkontrollnetz b gegebenen
Fläche, für den Parameterbereich
![]() u0
u0![]() u1
u1![]() v0
v0![]() v1
v1![]() . isolines wird rekursiv aufgerufen, um Unterschiede
in der Dichte der Linien auszugleichen. Dabei sollte aber die maximale
Rekursionstiefe möglichst klein gewählt werden. Der erste Aufruf
erfolgt natürlich für den Parameterbereich
. isolines wird rekursiv aufgerufen, um Unterschiede
in der Dichte der Linien auszugleichen. Dabei sollte aber die maximale
Rekursionstiefe möglichst klein gewählt werden. Der erste Aufruf
erfolgt natürlich für den Parameterbereich ![]() .
.
| isolines |
| Isolinien Plotter |
Wie in Abbildung 2.15 gezeigt, unterteilen wir den Parameterbereich in Quadrate solange, bis nur noch maximal eine Linie durch jede Seite des Quadrats geht. Haben wir vorher die maximale Rekursionstiefe erreicht, dann legen wir über das Quadrat im Parameterbereich noch einmal ein Gitter, damit wir wieder Quadrate erhalten, durch deren Seiten maximal eine Linie geht. Das Gitter wird durch die Variablen aus Schritt refit:KuF:bilinf bestimmt. Es gibt zusätzlich den Parameter maxlines zur Begrenzung der Anzahl der Linien, die pro Quadrat des letzten Rekursionsschritts gezeichnet werden. Damit wird verhindert, daß hier ein zu feines Gitter erzeugt wird. Die Funktionswerte auf diesem Gitter werden durch bilineare Interpolation approximiert. Vor allem bei äquidistanten Isolinien für Funktionen, bei denen die Werte in einzelnen Bereichen stark ansteigen oder abfallen, aber sich sonst eher gering verändern, verbessert dies das Verhalten des Algorithmus'.
Die Interpolationsformel für die bilineare Interpolation von ![]() auf dem Quadrat
auf dem Quadrat
![]() bei Schritt I-C
im Algorithmus lautet
bei Schritt I-C
im Algorithmus lautet
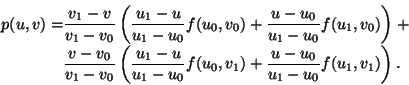 |
(2.80) |
Die Linien für ein einzelnes Quadrat werden schließlich durch den Algorithmus handle_quad gezeichnet. Hier wird einfach überprüft, von welcher Seite des Quadrats zu welcher Seite wir eine Linie zeichnen müssen. Dazu wird das Quadrat zusätzlich in zwei Dreiecke aufgeteilt und der Schnittpunkt mit der Diagonalen berücksichtigt. Optional kann die Linie auch noch in der Farbe für den für sie vorgesehenen Funktionswert gezeichnet werden. Außerdem kann man die Linien längs der Einheitsnormalen der Fläche um einen festen Wert verschieben, um sicherzustellen, daß sie nicht von der Fläche überdeckt werden.
| handle_quad |
| Isolinien für ein einzelnes Teilquadrat zeichnen |
Wir zerlegen zunächst das Quadrat in zwei Dreiecke über die Diagonale von (u1,v0) nach (u0,v1). In beiden Dreiecken überprüfen wir dann, von welcher Seite zu welcher Seite wir eventuell eine Linie ziehen müssen. Diese Linie wird auf dem Bézierflächenstück der Fläche, welches zum Bézierkontrollnetz der Funktion gehört, zu den entsprechenden Parameterwerten gezeichnet. Falls eine Isolinie durch eine der Seiten im Parameterbereich geht, wird der genaue Parameterwert durch lineare Interpolation auf der Seite berechnet. In Abbildung 2.16 sind die drei Fälle für das Dreieck (u0,v0), (u1,v0), (u0,v1) dargestellt.
Der Test, ob durch eine Seite eine Isolinie geht, hängt von der Weise ab, wie die Funktionswerte für die Isolinien gegeben wurden. Verwenden wir äquidistante Linien, wird handle_quad bereits mit den auf ganzzahlige Werte verschobenen und skalierten Funktionswerten aufgerufen. Wir müssen dann nur noch überprüfen, ob zwischen zwei Funktionswerten eine ganze Zahl liegt. Für eine Liste von Funktionswerten ist dies nicht ganz so einfach. Hierfür müssen wir für jedes Element dieser Liste überprüfen, ob es zwischen den zwei Funktionswerten an den Ecken liegt. Wenn wir die Liste der Funktionswerte sortieren, können wir dabei ein paar Vergleiche einsparen.
Mit Hilfe des Isolinien-Algorithmus' können wir auch Contourplots erstellen. Dazu verwenden wir für die Kontrollpunkte der Fläche ein ebenes Gitter. Auf diesem Gitter geben wir die Funktionskontrollpunkte für den Contourplot an. Zeichnen wir die Isolinien für diese Funktion, erhalten wir einen Contourplot. So können wir die Funktionskontrollpunkte z.B. über die Parametrisierung des Affensattels
In Abbildung 2.19 stellen wir die
Funktion
![]() auf der in
Abbildung 1.22 vorgestellten verdrehten Acht dar. Der
Ursprung liegt dabei “links hinten” in der Ecke des entsprechenden
erzeugenden Würfels. Ein Contourplot auf einer Ebene ist für diese
Funktion nicht mehr möglich.
auf der in
Abbildung 1.22 vorgestellten verdrehten Acht dar. Der
Ursprung liegt dabei “links hinten” in der Ecke des entsprechenden
erzeugenden Würfels. Ein Contourplot auf einer Ebene ist für diese
Funktion nicht mehr möglich.
Neben den Isolinien für Funktionen können wir sie auch für die Fläche selbst zeichnen, d.h. wir verwenden die Flächenfunktion selbst für Isolinien. In diesem Fall markieren die Isolinien die Kurven auf der Fläche mit konstantem Abstand vom Ursprung. Abbildung 2.20 zeigt dies für das in Abbildung 1.23 vorgestellte Kreuz. Der Ursprung wurde dabei in den Mittelpunkt des Kreuzes gelegt.
Interessanter sind aber Reflektionslinien. Dazu definieren wir
zunächst eine Ebene im Raum über einen Punkt ![]() und zwei linear
unabhängige Vektoren
und zwei linear
unabhängige Vektoren ![]() und
und ![]() . Auf dieser Ebene seien nun
parallele Lichtquellen im gleichen Abstand angebracht. In unserem
einfachen Modell sind die Lichtquellen unendlich lang und besitzen
keine Breite. Weiter nehmen wir an, daß die Intensität der
Lichtstrahlen unabhängig von der Entfernung immer gleich groß sei.
. Auf dieser Ebene seien nun
parallele Lichtquellen im gleichen Abstand angebracht. In unserem
einfachen Modell sind die Lichtquellen unendlich lang und besitzen
keine Breite. Weiter nehmen wir an, daß die Intensität der
Lichtstrahlen unabhängig von der Entfernung immer gleich groß sei.
![]() gebe die Richtung der Lichtquellen an und
gebe die Richtung der Lichtquellen an und ![]() sei der Abstand
zwischen den parallelen Lichtquellen. Das Licht von diesen
Lichtquellen reflektieren wir an der Fläche
sei der Abstand
zwischen den parallelen Lichtquellen. Das Licht von diesen
Lichtquellen reflektieren wir an der Fläche ![]() für einen
vorgegebenen Beobachtungspunkt
für einen
vorgegebenen Beobachtungspunkt ![]() . Diese Situation ist schematisch in
Abbildung 2.21 dargestellt.
. Diese Situation ist schematisch in
Abbildung 2.21 dargestellt.
Sei ![]() ein beliebiger Punkt auf
ein beliebiger Punkt auf ![]() . Die Strecke
. Die Strecke ![]() legt den
Ausfallswinkel für einen Reflektionsstrahl fest. Da der Einfallswinkel
genauso groß wie der Ausfallswinkel sein muß, erhalten wir die
Richtung
legt den
Ausfallswinkel für einen Reflektionsstrahl fest. Da der Einfallswinkel
genauso groß wie der Ausfallswinkel sein muß, erhalten wir die
Richtung ![]() des Reflektionsstrahls aus
des Reflektionsstrahls aus
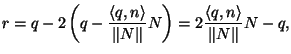 |
(2.82) |
| (2.83) |
![[p_1, p_2, -r] [t_1; t_2; s] = Q - P.](img610.png) |
(2.84) |
Die Reflektionslinien können wir über den Isolinien-Algorithmus
zeichnen, indem wir ![]() in Abhängigkeit von
in Abhängigkeit von ![]() als Funktionswert
verwenden. Auch wenn es kein realistisches Reflektionsmodell ist, kann
man über diese Reflektionslinien sehr schön kleine Unebenheiten,
etc. in der Fläche erkennen. Wichtig ist allerdings dabei eine
sinnvolle Wahl der Ebene und des Beobachtungspunktes. Es genügt auch
meistens nicht, die Fläche nur mit einer Einstellung zu untersuchen.
als Funktionswert
verwenden. Auch wenn es kein realistisches Reflektionsmodell ist, kann
man über diese Reflektionslinien sehr schön kleine Unebenheiten,
etc. in der Fläche erkennen. Wichtig ist allerdings dabei eine
sinnvolle Wahl der Ebene und des Beobachtungspunktes. Es genügt auch
meistens nicht, die Fläche nur mit einer Einstellung zu untersuchen.
Abbildung 2.22 zeigt die Reflektionslinien für ein Fläche, deren Kontrollpunkte über das hyperbolische Paraboloid
![(u,v) -> [u; v; uv]](img612.png) mit mit |
(2.85) |
Abbildung 2.23 zeigt die Reflektionslinien für
Irregularitäten der Ordnung ![]() ,
, ![]() und
und ![]() . Die Irregularitäten
liegen alle um den Punkt
. Die Irregularitäten
liegen alle um den Punkt
![]() und
die Reflektionsebene ist durch den Punkt
und
die Reflektionsebene ist durch den Punkt
![]() , den Lichtquellenrichtungsvektor
, den Lichtquellenrichtungsvektor
![]() und den Abstandsvektor
und den Abstandsvektor
![]() gegeben. Für die
Irregularitäten der Ordnung
gegeben. Für die
Irregularitäten der Ordnung ![]() und
und ![]() wurde resolution auf
wurde resolution auf
![]() , maxlevel auf
, maxlevel auf ![]() undmaxlines auf
undmaxlines auf ![]() gesetzt.
Für die Irregularität der Ordnung
gesetzt.
Für die Irregularität der Ordnung ![]() war
resolution
war
resolution![]() ,
maxlevel
,
maxlevel![]() und
maxlines
und
maxlines![]() .
.
Für die in Abbildung 1.21 vorgestellte Acht zeigt
Abbildung 2.24 die Reflektionslinien für
eine zur ![]() -
-![]() -Ebene parallelen Ebene über der Acht. Aufgrund der
Irregularitäten sind diese sehr unregelmäßig. Auch ist es notwendig
maxlines und maxlevel des Isolinien-Algorithmus'
stark zu beschränken, um unnötigen Rechenaufwand am Rand des
Reflektionsgebietes zu vermeiden. maxlevel wurde für diese
Abbildung auf
-Ebene parallelen Ebene über der Acht. Aufgrund der
Irregularitäten sind diese sehr unregelmäßig. Auch ist es notwendig
maxlines und maxlevel des Isolinien-Algorithmus'
stark zu beschränken, um unnötigen Rechenaufwand am Rand des
Reflektionsgebietes zu vermeiden. maxlevel wurde für diese
Abbildung auf ![]() , maxlines auf 6 und resolution
auf
, maxlines auf 6 und resolution
auf ![]() gesetzt.
gesetzt.