Als spezielle Funktionen betrachten wir abschließend die Krümmung von Flächen. Wir geben hier nur eine kurzen Überblick aus der Differentialgeometrie. Für eine umfassende Einführung sei beispielsweise auf [Car93] verwiesen, aus dem folgender kurzer Überblick zusammengestellt wurde.
Es sei
![]() eine reguläre Fläche und
eine reguläre Fläche und ![]() ein Punkt
auf dieser Fläche. Wir bezeichnen die Menge der Tangentenvektoren von
allen Kurven in
ein Punkt
auf dieser Fläche. Wir bezeichnen die Menge der Tangentenvektoren von
allen Kurven in ![]() durch
durch ![]() als Tangentialebene
als Tangentialebene ![]() an
an ![]() in
in
![]() . Das natürliche innere Produkt in
. Das natürliche innere Produkt in
![]() induziert auf
jedem
induziert auf
jedem ![]() ein inneres Produkt
ein inneres Produkt
![]() . Dieses wird als
eine symmetrische Bilinearform
. Dieses wird als
eine symmetrische Bilinearform
![]() mit
mit
![]() dargestellt. Wir bezeichnen
dargestellt. Wir bezeichnen ![]() als erste
Fundamentalform von
als erste
Fundamentalform von ![]() in
in ![]() .
.
Für ein
![]() existiert nach Definition eine Kurve
existiert nach Definition eine Kurve
![]() auf
auf ![]() für
für
![]() mit
mit
![]() , so daß
, so daß ![]() und
und ![]() gilt. Dies
liefert die folgende Form für
gilt. Dies
liefert die folgende Form für ![]() :
:
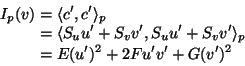 |
(2.86) |
Ist
![]() eine nach der Bogenlänge
eine nach der Bogenlänge
![]() parametrisierte Kurve, dann ist
parametrisierte Kurve, dann ist
![]() die Krümmung von
die Krümmung von
![]() in
in ![]() . Hieraus leiten wir die Krümmung für die Fläche
. Hieraus leiten wir die Krümmung für die Fläche ![]() ab.
Sei
ab.
Sei
![]() die Abbildung, die jedem Punkt
die Abbildung, die jedem Punkt ![]() von
von ![]() den Einheitsnormalenvektor
zuweist.
den Einheitsnormalenvektor
zuweist. ![]() gibt so für jeden Punkt und damit für die ganze Fläche
eine Orientierung an. Die Werte der Abbildung
gibt so für jeden Punkt und damit für die ganze Fläche
eine Orientierung an. Die Werte der Abbildung
![]() liegen
alle in der Einheitssphäre
liegen
alle in der Einheitssphäre
![]() .
Somit können wir die Gauß-Abbildung von
.
Somit können wir die Gauß-Abbildung von ![]() als
als
![]() definieren. Diese Abbildung ist für orientierbare Flächen
differenzierbar und das Differential
definieren. Diese Abbildung ist für orientierbare Flächen
differenzierbar und das Differential ![]() von
von ![]() ist eine lineare
Abbildung von
ist eine lineare
Abbildung von ![]() in den Tangentenraum
in den Tangentenraum
![]() . Nachdem
beide Tangentenräume parallele Ebenen sind, kann man
. Nachdem
beide Tangentenräume parallele Ebenen sind, kann man ![]() auch als
lineare Abbildung auf
auch als
lineare Abbildung auf ![]() interpretieren. Weiter können wir
hiermit die zweite Fundamentalform von
interpretieren. Weiter können wir
hiermit die zweite Fundamentalform von ![]() bei
bei ![]() als
als
![]() definieren.
definieren.
Wir betrachten wieder eine reguläre, nach Bogenlänge ![]() parametrisierte Kurve
parametrisierte Kurve ![]() , die ganz in
, die ganz in ![]() verläuft und es gelte
verläuft und es gelte ![]() .
. ![]() sei die Krümmung von
sei die Krümmung von ![]() in
in ![]() und
und ![]() sei der
Normalenvektor an
sei der
Normalenvektor an ![]() . Dann ist
. Dann ist
![]() die Normalkrümmung
von
die Normalkrümmung
von ![]() in
in ![]() . Wir betrachten nun alle Kurven in
. Wir betrachten nun alle Kurven in ![]() durch
durch ![]() . Die
maximale und minimale Normalkrümmung heißen Hauptkrümmungen von
. Die
maximale und minimale Normalkrümmung heißen Hauptkrümmungen von ![]() bei
bei ![]() . Weiter definieren wir die Gauß'sche Krümmung als Determinante
von
. Weiter definieren wir die Gauß'sche Krümmung als Determinante
von ![]() und der negative Wert der halben Spur von
und der negative Wert der halben Spur von ![]() heißt die
mittlere Krümmung.
heißt die
mittlere Krümmung.
Zur Vereinfachung der Notation stehen im folgenden die Funktionen für
ihren Wert im Punkt ![]() . Es gilt
. Es gilt
| (2.88) | ||
| (2.89) |
| (2.91) |
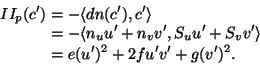 |
(2.92) |
| (2.94) |
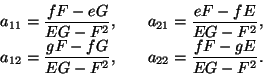 |
(2.95) |
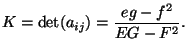 |
(2.96) |
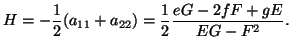 |
(2.97) |
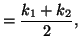 |
(2.98) | |
| (2.99) |
| (2.100) |
| (2.101) |
Berechnen wir ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() über (2.87)
und (2.93), dann erhalten wir über obige Formeln die
verschiedenen Krümmungen zu einem Punkt
über (2.87)
und (2.93), dann erhalten wir über obige Formeln die
verschiedenen Krümmungen zu einem Punkt ![]() . Damit können wir die
Krümmungsfunktionen einfach implementieren, indem wir die Auswertung
der Bézierkontrollnetze für die Funktion durch die Berechnung von
. Damit können wir die
Krümmungsfunktionen einfach implementieren, indem wir die Auswertung
der Bézierkontrollnetze für die Funktion durch die Berechnung von ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() und der entsprechenden Krümmung für das
Bézierkontrollnetz der Fläche ersetzen.
und der entsprechenden Krümmung für das
Bézierkontrollnetz der Fläche ersetzen.
Wir stoßen hier allerdings auch an die Grenzen der biquadratischen
G-Splines. Biquadratische Splineflächen können nur tangential stetig
zusammengesetzt werden. Für die Krümmungen benötigen wir aber auch die
zweiten Ableitungen zur Berechnung von ![]() ,
, ![]() und
und ![]() . Deshalb
müssen die Krümmungsfunktionen nicht mehr stetig sein. Besonders wird
dies an den irregulären Stellen des Kontrollnetzes sichtbar.
. Deshalb
müssen die Krümmungsfunktionen nicht mehr stetig sein. Besonders wird
dies an den irregulären Stellen des Kontrollnetzes sichtbar.
In Abbildung 2.25 stellen wir die Gauß-Krümmung
in der Umgebung von Irregularitäten der Ordnung ![]() ,
, ![]() und
und ![]() dar.
Nachdem die Formeln für biquadratische G-Splines an den
Irregularitäten nur aus den Bedingungen für tangentiales
Zusammensetzen der Flächenstücke erzeugt wurden, ist die Krümmung
natürlich nicht stetig. Für die Stetigkeit der Krümmung benötigen wir
Splineflächen höherer Ordnung.
dar.
Nachdem die Formeln für biquadratische G-Splines an den
Irregularitäten nur aus den Bedingungen für tangentiales
Zusammensetzen der Flächenstücke erzeugt wurden, ist die Krümmung
natürlich nicht stetig. Für die Stetigkeit der Krümmung benötigen wir
Splineflächen höherer Ordnung.
Für die über die Parametrisierung des Whitneyschen Regenschirms erzeugte Fläche aus Abbildung 2.5 zeigen wir in Abbildung 2.26 die Gauß'sche und die mittlere Krümmung.
Abbildung 2.27 zeigt die Gauß'sche Krümmung der in Abbildung 1.24 vorgestellten T-Fläche. Neben der Farbdarstellung stellen wir sie hier auch als farbige Fläche über dem T dar.
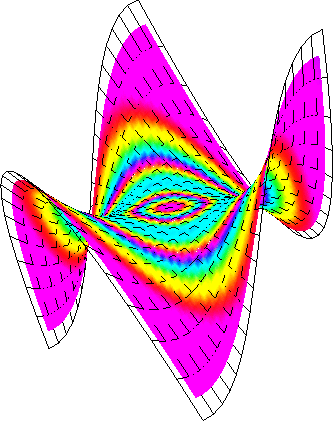
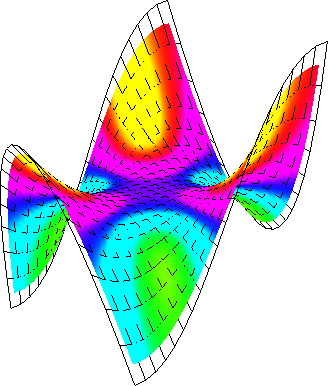
Abbildung 2.28 zeigt die Gauß'sche und die mittlere Krümmung der Fläche, deren Kontrollpunkte über die Parametrisierung (2.81) des Affensattels festgelegt wurden. Besonders bei der mittleren Krümmung erkennt man, daß die Funktion nicht mehr stetig ist. Die exakten Formeln für die Krümmungen des Affensattels sind
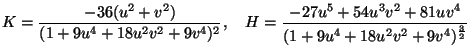 |
(2.102) |
|