S O’Neil, FC Langbein, E Jonckheere, SG Shermer.
We use the following two datasets in this paper: FC Langbein, SP O’Neil, SG Shermer. Data – Energy Landscape Controllers for XX Spin Rings. Dataset, Version 1.0, 2023. https://qyber.black/spinnet/data-elc-xx-rings. FC Langbein, SP O’Neil, SG Shermer. Results – Energy Landscape Controllers for XX Spin Rings – Robustness. Dataset, Version 1.0, 2023. https://qyber.black/spinnet/results-elc-xx-rings-robustness.
Research Directions: Quantum Technologies, 1, E13, 2023.
[DOI:10.1017/qut.2023.6]
[arXiv:2303.05649]
[PDF]
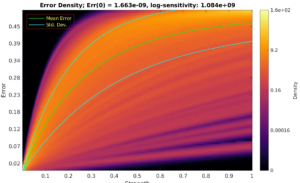
As shown in previous work, in some cases closed quantum systems exhibit a non-conventional trade-off in performance and robustness in the sense that controllers with the highest fidelity can also provide the best robustness to parameter uncertainty. As the dephasing induced by the interaction of the system with the environment guides the evolution to a more classically mixed state, it is worth investigating what effect the introduction of dephasing has on the relationship between performance and robustness. In this paper we analyze the robustness of the fidelity error, as measured by the logarithmic sensitivity function, to dephasing processes. We show that introduction of dephasing as a perturbation to the nominal unitary dynamics requires a modification of the log-sensitivity formulation used to measure robustness about an uncertain parameter with non-zero nominal value used in previous work. We consider controllers optimized for a number of target objectives ranging from fidelity under coherent evolution to fidelity under dephasing dynamics to determine the extent to which optimizing
for a specific regime has desirable effects in terms of robustness. Our analysis is based on two independent computations of the log-sensitivity: a statistical Monte Carlo approach and an analytic calculation. We show that despite the different log-sensitivity calculations employed in this study, both demonstrate that the log-sensitivity of the fidelity error to dephasing results in a conventional trade-off between performance and robustness.![]() This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Robustness of Energy Landscape Control to Dephasing
Cite this page as 'Frank C Langbein, "Robustness of Energy Landscape Control to Dephasing," Ex Tenebris Scientia, 19th March 2023, https://langbein.org/analysis-dataset2/ [accessed 1st January 2026]'.
