Sean O’Neil, Edmond Jonckheere, Sophie Schirmer, Frank Langbein. Sensitivity and Robustness of Quantum Spin-1/2 Rings to Parameter Uncertainty. Proc. IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, pp. 6137-6142, 2017. [DOI:10.1109/CDC.2017.8264584] [arXiv:1708.09649] [PDF]
Metrics for the case of a 1 to 6 transfer and
coupling uncertainty between spins 5 and 6.
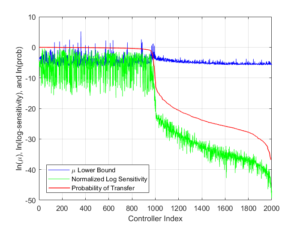
Selective transfer of information between spin-1/2 particles arranged in a ring is achieved by optimizing the transfer fidelity over a readout time window via shaping, externally applied, static bias fields. Such static control fields have properties that clash with the expectations of classical control theory. Previous work has shown that there are cases in which the logarithmic differential sensitivity of the transfer fidelity to uncertainty in coupling strength or spillage of the bias field to adjacent spins is minimized by controllers that produce the best fidelity. Here we expand upon these examples and examine cases of both classical and non-classical behavior of logarithmic sensitivity to parameter uncertainty and robustness as measured by the μ function for quantum systems. In particular we examine these properties in an 11-spin ring with a single uncertainty in coupling strength or a single bias spillage.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.