Xianfang Sun, Paul L. Rosin, Ralph R. Martin, Frank C. Langbein. Random Walks for Feature-Preserving Mesh Denoising. Computer-Aided Geometric Design [Solid and Physical Modeling – Selected papers from the Solid and Physical Modeling and Applications Symposium 2007 (SPM 2007)], 25(7):437-456, 2008. [DOI:10.1016/j.cagd.2007.12.008] [PDF]
sun2008
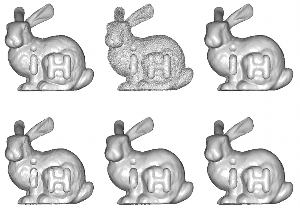
An approach to mesh denoising based on the concept of random walks is examined. The proposed method consists of two stages: face normal filtering, followed by vertex position updating to integrate the denoised face normals in a least-squares manner. Face normal filtering is performed by weighted averaging of normals in a neighbourhood. A novel approach to determining weights is to compute the probability of arriving at each neighbour following a fixed-length random walk of a virtual particle starting at a given face of the mesh. The probability of the particle stepping from its current face to some neighbouring face is a function of the angle between the two face normals, based on a Gaussian distribution whose variance is adaptively adjusted to enhance the feature-preserving property of the algorithm. The vertex position updating procedure uses the conjugate gradient algorithm for speed of convergence. Analysis and experiments show that random walks of different step lengths yield similar denoising results. Our experiments show that, in fact, iterative application of a one-step random walk in a progressive manner effectively preserves detailed features while denoising the mesh very well. This approach is faster than many other feature-preserving mesh denoising algorithms.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.