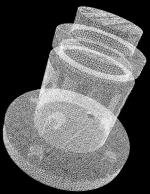
To obtain the initial data for a part we use a commercial 3D laser scanner. From the generated point clouds a valid CAD model can be created by using existing technologies. This can be done by segmentation of the point sets into subsets and by finding surfaces that best approximate those subsets. From these surfaces a valid boundary representation model can be created.
- Data Acquisition
- Multiple 3D point clouds representing different views of the object are obtained from a laster scanner.
- The multiple views are registered into a single set of points using an ICRP registration method.
- Segmentation
- The point cloud is split into subsets representing natural surfaces of the object.
- Surface Fitting
- For each point subset an appropriate surface type is determined
- A surface of this type is fitted to the point set
- At this point we only consider objects with planar, spherical cylindrical, conical and toroidal surfaces
- Model Creation
- An initial solid model is created by stitching the generated surfaces
- This initial model suffers from various naccuracies caused by
- sensing errorsapproximation and numerical errors
- possible wear of the object
- manufacturing method used to make the object
- Beautification
- As our goal is to automatically reconstruct an ideal model with desired geometric regularities, those regularities have to be enforced at some stage of the process. In our approach we add a post-processing step called beautification. For this the initial model is analysed to find geometric regularities and then an improved model is reconstructed using geometric constraints.
Example
Our Strategy for Beautification
To ensure that the model generated by the system exhibits certain geometric regularities we add a post-processing step, which we call beautification. In this step the initially created boundary representation model is analysed for regularities and a suitable subset of regularities is selected to generate an improved model using geometric constraints.
Below we outline the strategy and concepts for the main modules of our beautification system. For more details please see the publications and presentations. First the initial model is analysed for geometric regularities which are then used by a hypothesizer which selects a suitable subset of the regularities and enforces them on the model using geometric constraints. In the final step the model is reconstructed from the solution of the geometric constraint system also considering the combinatorial (topological) structure of the initial model.
Analyser
We detect a large set of potential geometric regularities which are approximately present in the initial model. The regularities are described in terms of similarities. Different properties of faces, edges and vertices, and small groups of these elements in a boundary representation model are represented as feature objects. Similar feature objects, such as directions which are parallel, form one sort of regularities. For each group of similar feature objects, special feature objects which might represent the group form further regularities, e.g. an integer value which approximates the radius of similar cylinders. Further regularities arise from symmetries of feature object sets. These can be complete or partial symmetries of the object itself or symmetries of the features in special feature spaces, like symmetrically arranged directions in a direction space.
Hypothesizer
The hypothesizer has to select a suitable set of consistent geometric regularities which include at least the major desired regularities of the ideal design for the initial model. We express the regularities in terms of geometric constraints. The hypothesizer consists of a selection module which selects desirable constraints such that the whole constraint system remains consistent and a constraint solver module which tries to solve the selected constraint system. Both modules cannot be separated from each other. The selection module tries to select desirable constraint sets while the solver module is responsible for checking the solvability of the system. There are different strategies in combining the selection and solving method. We can either keep them separate trying to solve a pre-selected system and adjust the selection according to the solvability of the system or we can consecutively select constraints and check if the system remains solvable and eventually also simplify the system if solvable sub-systems are detected.
Constraint Selection
The constraints are grouped in sets each describing a single regularity. Based on the general desirability of a certain regularity and how well the regularity is present in the initial model the constraint sets are prioritised. We always select constraints in these sets. Based on the priority the constraint selection module tries to select a consistent set of desirable constraints. The consistency is checked by the constraint solver and some simple geometric reasoning for obviously inconsistent constraints, such as two constraints on the same geometric objects with different constants.
Constraint Solver
The constraint solver tries to find a solution to the selected constraint system and is primarily responsible for reporting contradictory constraints in the system. We consider graph-based as well as purely numerical methods (using numerical optimization) to find a solvable system. For the numerical methods we initially select a constraint system consisting of highly desirable constraints which do not have any obvious contradictions. We try to solve the system and if this fails we adjust the constraint selection. The graph-based methods are used to consecutively build up the constraint system selecting the most desirable constraints without creating inconsistencies or over-constraint systems. When a solvable sub-system in the constraint graph has been detected we can solve it and replace it by a simpler element in the graph.
Reconstruction
From the solution of the final constraint system selected by the hypothesizer and the combinatorial structure of the initial model an improved model is reconstructed. In addition we can fix problems in the combinatorial structure, align the model with the coordinate axes, etc.
Acknowledgements
We implemented some of the reverse engineering methods, but the main part of the software for creating the initial model was provided by T. Varady from the Hungarian Academy of Sciences and CADMUS Consulting and Development Ltd. Our main contributions are the concepts and software for beautification.
![]() This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.