E. Jonckheere, S. G. Schirmer, F.C. Langbein. Jonckheere-Terpstra test for nonclassical error versus log-sensitivity relationship of quantum spin network controllers. Int J Robust and Nonlinear Control, 28(6):2383-2403, 2018. [DOI:10.1002/rnc.4022] [arXiv:1612.02784] [PDF]
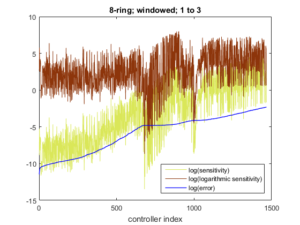
Selective information transfer in spin ring networks by energy landscape shaping control has the property that the error 1-prob, where prob is the transfer success probability, and the sensitivity of the error to spin coupling uncertainties are statistically increasing across a family of controllers of increasing error. The need for a statistical Hypothesis Testing of a concordant trend is made necessary by the noisy behavior of the sensitivity versus the error as a consequence of the optimization of the controllers in a challenging error landscape. Here, we examine the concordant trend between the error and another measure of performance—the logarithmic sensitivity—used in robust control to formulate a well known fundamental limitation. Contrary to error versus sensitivity, the error versus logarithmic sensitivity trend is less obvious, because of the amplification of the noise due to the logarithmic normalization. This results in the Kendall τ test for rank correlation between the error and the log sensitivity to be somewhat pessimistic with marginal significance level. Here it is shown that the Jonckheere-Terpstra test, because it tests the Alternative Hypothesis of an ordering of the medians of some groups of log sensitivity data, alleviates this statistical problem. This identifies cases of concordant trend between the error and the logarithmic sensitivity, a highly anti-classical features that goes against the well know sensitivity versus complementary sensitivity limitation.
Featured in Can controllers for quantum systems beat classical limits of robustness? on Andvances in Engineering.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.