Quantum networks: Anti-core of spin chains

E. Jonckheere, F. C. Langbein, S. Schirmer. Quantum networks: Anti-core of spin chains. Quantum Information Processing. 13(7):1607-1637, 2014. [DOI:10.1007/s11128-014-0755-5] [arXiv:1403.0159] [PDF]

mtp

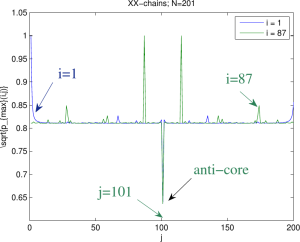
The purpose of this paper is to exhibit a quantum network phenomenon – the anti-core—that goes against the classical network concept of congestion core. Classical networks idealized as infinite, Gromov hyperbolic spaces with least-cost path routing (and subject to a technical condition on the Gromov boundary) have a congestion core, defined as a subnetwork that routing paths have a high probability of visiting. Here, we consider quantum networks, more specifically spin chains, define the so-called maximum excitation transfer probability between spin and spin , and show that the central spin has among all other spins the lowest probability of being excited or transmitting its excitation. The anti-core is singled out by analytical formulas for , revealing the number theoretic properties of quantum chains. By engineering the chain, we further show that this probability can be made vanishingly small.

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.