F. C. Langbein, A. D. Marshall, R. R. Martin. Numerical Methods for Beautification of Reverse Engineered Geometric Models. In: H. Suzuki, R. R. Martin (eds), Proc. Geometric Modeling and Processing, IEEE Computer Society, pp. 159-168, 2002. [DOI:10.1109/GMAP.2002.1027507] [PDF]
langbein2002
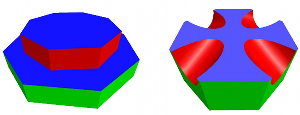
Boundary representation models reconstructed from 3D range data suffer from various inaccuracies caused by noise in the data and the model building software. The quality of such models can be improved in a beautification step, which finds geometric regularities approximately present in the model and tries to impose a consistent subset of these regularities on the model. A framework for beautification and numerical methods to select and solve a consistent set of constraints deduced from a set of regularities are presented. For the initial selection of consistent regularities likely to be part of the model’s ideal design priorities, and rules indicating simple inconsistencies between the regularities are employed. By adding regularities consecutively to an equation system and trying to solve it using quasi-Newton optimization methods, inconsistencies and redundancies are detected. The results of experiments are encouraging and show potential for an expansion of the methods based on degree of freedom analysis.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.