Time Domain Sensitivity of the Tracking Error

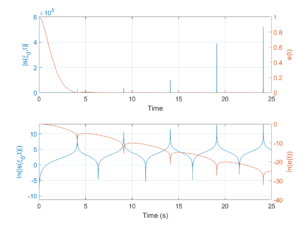A strictly time-domain formulation of the log-sensitivity of the error signal to structured plant uncertainty is presented and analyzed through simple classical and quantum systems. Results demonstrate that across a wide range of physical systems, maximization of performance (minimization of the error signal) asymptotically or at a specific time comes at the cost of increased log-sensitivity, implying a time-domain constraint analogous to the frequency-domain identity S(s) + T(s) = I. While of limited value in classical problems based on asymptotic stabilization or tracking, such a time-domain formulation is valuable in assessing the reduced robustness cost concomitant with high-fidelity quantum control schemes predicated on time-based performance measures.

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.