Statistically Characterising Robustness and Fidelity of Quantum Controls and Quantum Control Algorithms

I. Khalid, C. A. Weidner, E. A. Jonckheere, S. G. Shermer, F. C. Langbein. Statistically Characterising Robustness and Fidelity of Quantum Controls and Quantum Control Algorithms. Phys. Rev. A, 107, 032606, 2023. [DOI:10.1103/PhysRevA.107.032606] [arXiv:2207.07801] [PDF]

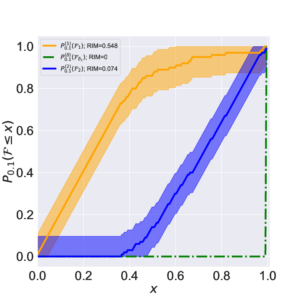
Robustness of quantum operations or controls is important to build reliable quantum devices. The robustness-infidelity measure (RIM_p) is introduced to statistically quantify in a single measure the robustness and fidelity of a controller as the p-th order Wasserstein distance between the fidelity distribution of the controller under any uncertainty and an ideal fidelity distribution. The RIM_p is the p-th root of the p-th raw moment of the infidelity distribution. Using a metrization argument, we justify why RIM₁ (the average infidelity) is a good practical robustness measure. Based on the RIM_p, an algorithmic robustness-infidelity measure (ARIM) is developed to quantify the expected robustness and fidelity of controllers found by a control algorithm. The utility of the RIM and ARIM is demonstrated on energy landscape controllers of spin-1/2 networks subject to Hamiltonian uncertainty. The robustness and fidelity of individual controllers as well as the expected robustness and fidelity of controllers found by different popular quantum control algorithms are characterized. For algorithm comparisons, stochastic and non-stochastic optimization objectives are considered. Although high fidelity and robustness are often conflicting objectives, some high-fidelity, robust controllers can usually be found, irrespective of the choice of the quantum control algorithm. However, for noisy or stochastic optimization objectives, adaptive sequential decision-making approaches, such as reinforcement learning, have a cost advantage compared to standard control algorithms and, in contrast, the high infidelities obtained are more consistent with high RIM values for low noise levels.

The code associated with this work is available at:

I. Khalid, C. A. Weidner, E. A. Jonckheere, S. G. Shermer, F. C. Langbein. RobChar: Robust Characterisation of Quantum Controls and Control Algorithms. Code, https://github.com/qyber-black/code-robchar, 2022. [DOI:10.5281/zenodo.6891152] [Project]

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.