Sophie G. Schirmer, Frank C. Langbein, Carrie A. Weidner, Edmond Jonckheere. Robust Control Performance for Open Quantum Systems. IEEE Trans Automatic Control, 67(11):6012-6024, 2022. [DOI:10.1109/TAC.2022.3181249] [arXiv:2008.13691] [PDF]
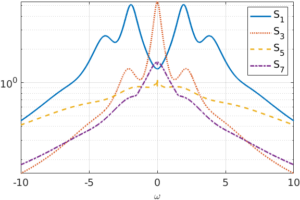
Error gains as a function of frequency for structured uncertainties.
Robust performance of control schemes for open quantum systems is investigated under classical uncertainties in the generators of the dynamics and nonclassical uncertainties due to decoherence and initial state preparation errors. A formalism is developed to measure performance based on the transmission of a dynamic perturbation or initial state preparation error to the quantum state error. This makes it possible to apply tools from classical robust control such as structured singular value analysis. A difficulty arising from the singularity of the closed-loop Bloch equations for the quantum state is overcome by introducing the #-inversion lemma, a specialized version of the matrix inversion lemma. Under some conditions, this guarantees continuity of the structured singular value at s = 0. Additional difficulties occur when symmetry gives rise to multiple open-loop poles, which under symmetry-breaking unfold into single eigenvalues. The concepts are applied to systems subject to pure decoherence and a general dissipative system example of two qubits in a leaky cavity under laser driving fields and spontaneous emission. A nonclassical performance index, steady-state entanglement quantified by the concurrence, a nonlinear function of the system state, is introduced. Simulations confirm a conflict between entanglement, its log-sensitivity and stability margin under decoherence.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.