SG Schirmer, FC Langbein, CA Weidner, EA Jonckheere. Robustness of Quantum Systems Subject to Decoherence: Structured Singular Value Analysis?. IEEE Conf Decision and Control, pp. 4158-4163, 2021. [DOI:10.1109/CDC45484.2021.9682796] [arXiv:2110.05372] [PDF]
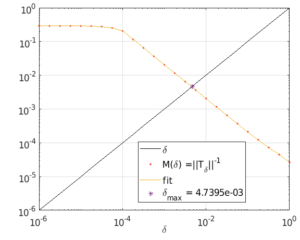We study the problem of robust performance of quantum systems under structured uncertainties. A specific feature of closed (Hamiltonian) quantum systems is that their poles lie on the imaginary axis and that neither a coherent controller nor physically relevant structured uncertainties can alter this situation. This changes for open systems where decoherence ensures asymptotic stability and creates a unique landscape of pure performance robustness, with the distinctive feature that closed-loop stability is secured by the underlying physics and needs not be enforced. This stability, however, is often detrimental to quantum-enhanced performance, and additive perturbations of the Hamiltonian give rise to dynamic generators that are nonlinear in the perturbed parameters, invalidating classical paradigms to assess robustness to structured perturbations such as singular value analysis. This problem is addressed using a fixed-point iteration approach to determine a maximum perturbation strength δmax that ensures that the transfer function remains bounded, ||Tδ|| < δ−1 for δ < δmax.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.