M. Li, F. C. Langbein, R. R. Martin. Detecting Approximate Symmetries of Discrete Point Subsets. Computer-Aided Design, 40(1):76-93, 2008. [DOI:10.1016/j.cad.2007.06.007] [PDF]
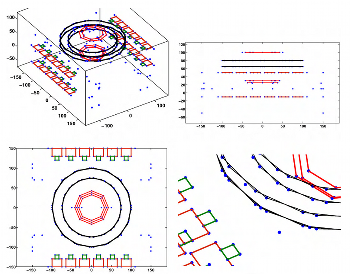
Constrained Design of Curves and Surfaces. Detecting approximate symmetries of parts of a model is important when attempting to determine the geometrical design intent of approximate boundary-representation (B-rep) solid models produced e.g. by reverse engineering systems. For example, such detected symmetries may be enforced exactly on the model to improve its shape, to simplify its analysis, or to constrain it during editing. We give an algorithm to detect local approximate symmetries in a discrete point set derived from a B-rep model: the output comprises the model’s potential local symmetries at various automatically detected tolerance levels. Non-trivial symmetries of subsets of the point set are found as unambiguous permutation cycles, i.e. vertices of an approximately regular polygon or an anti-prism, which are sufficiently separate from other points in the point set. The symmetries are detected using a rigorous, tolerance-controlled, incremental approach, which expands symmetry seed sets by one point at a time. Our symmetry cycle detection approach only depends on inter-point distances. The algorithm takes time O(n^4) where n is the number of input points. Results produced by our algorithm are demonstrated using a variety of examples.
![]() This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.