E. Jonckheere, S. G. Schirmer, F. C. Langbein, C. A. Weidner. Noiseless robust performance with structured uncertainties and initial state error. Preprint 2022. [PDF]
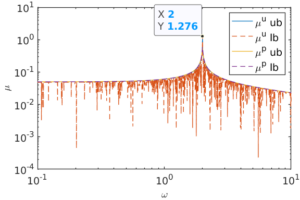A novel method to quantify robust performance is formulated for situations where structured parameter variations and initial state errors rather than extraneous noise are the main performance limiting factors. The central mathematical object is the error dynamics, the difference between nominal and perturbed dynamics, driven by the unperturbed or perturbed state, rather than an artificially imposed noise. The unperturbed versus perturbed dichotomy has the interpretation of the relative error dynamics scaled by either the unperturbed or perturbed dynamics. The unperturbed-driven error dynamics has the unique feature of decoupling the effect of physically meaningful uncertainties from additive noise. The perturbed case offers the possibility to side-step structured singular value or μ computations. Applications to a lightly damped mechanical system and a slowly dephasing quantum system demonstrate the usefulness of the concepts across a broad range of systems. Finally, a fixed point algorithm specifically developed for quantum systems with state transitions depending in a nonlinear fashion on uncertainties is proposed as the substitute for classical μ.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.