June 2005 – June 2009: Smoothing Boundary Curves. ESPRC GR/T24579/01. PI: R. R. Martin, CoI: F. C. Langbein. Industrial partner: Delcam Int PLC. £196.722.
February 2005 – February 2008: Reverse Engineering of Reliefs. EPSRC GR/T24425/01. PI: RR Martin, CoI: AD Marshall, FC Langbein, PL Rosin. Industrial partner: Delcam Int PLC. £200,425.
Reverse Engineering of Reliefs
A suitable watermarking scheme has to be sufficiently reliable such that it is feasible to use it as a mean to resolve disputes over ownership or origin of a particular object in the context of a court of law or similar situations. It should be infeasible to remove the watermark […]
Watermarking
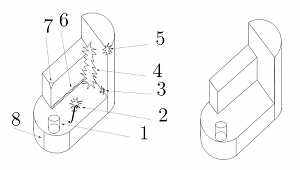
C. H. Gao, F. C. Langbein, A. D. Marshall, R. R. Martin. Local Topological Beautification of Reverse Engineered Models. Computer-Aided Design, 36(13):1337-1355, 2004. [DOI:10.1016/j.cad.2004.02.004] [PDF]
Local Topological Beautification of Reverse Engineered Models
C. H. Gao, F. C. Langbein, A. D. Marhall, R. R. Martin, Y. Li, Z. Yang. Partial Approximate Symmetry Detection of Geometric Model. Materials Science Forum, 471-472:702-706, 2004. [DOI:10.4028/0-87849-956-3.702]
Partial Approximate Symmetry Detection of Geometric Model
F. C. Langbein. Reverse Engineering: From Artifacts to Concepts. Public engagement and outreach talk given at various occasions. [PDF]
Reverse Engineering: From Artifacts to Concepts
F.C. Langbein. Design Intent of Geometric Models. Invited seminar talk, Institute of Information and Mathematical Sciences, Massey University at Albany, 22nd September 2004. [PDF]
Design Intent of Geometric Models
F. C. Langbein. Design Intent of Geometric Models. Invited seminar talk, Dept. Computer Science, Auckland University, 15th September 2004. [PDF]
Design Intent of Geometric Models
July 2004 – July 2007: Detection of Design Intent in Complex Approximate Geometric Models. EPSRC GR/S69085/01. PI: F. C. Langbein. £123,639.
Detection of Design Intent in Complex Approximate Geometric Models
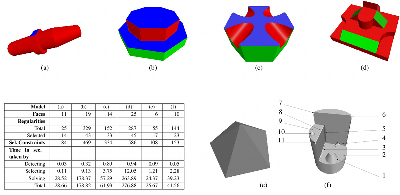
F. C Langbein, C. H. Gao, B. I. Mills, A. D. Marshall, R. R. Martin. Topological and Geometric Beautification of Reverse Engineered Geometric Models. In: G. Elber, P. Brunet (eds), Proc. ACM Symp. Solid Modelling and Applications, pp. 255-260, 2004. [DOI:10.13140/RG.2.1.1487.7523] [Proceedings] [PDF]
Topological and Geometric Beautification of Reverse Engineered Geometric Models
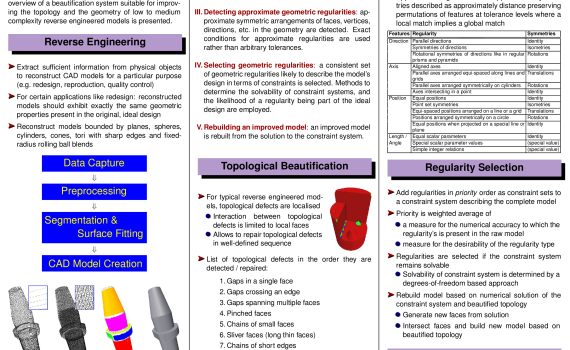
F. C. Langbein, C. H. Gao, B. I. Mills, A. D. Marshall, R. R. Martin. Topological and Geometric Beautification of Reverse Engineered Geometric Models. Poster, ACM Symp. Solid Modelling and Applications, Genova, Italy, 9-11 June, 2004. [PDF]
Topological and Geometric Beautification of Reverse Engineered Geometric Models

F. C. Langbein, A. D. Marshall, R. R. Martin. Choosing Consistent Constraints for Beautification of Reverse Engineered Geometric Models, Computer-Aided Design, 36(3):261-278, 2004. [DOI:10.1016/S0010-4485(03)00108-8] [PDF]
