M. Li, F. C. Langbein, R. R. Martin. Constructing Regularity Feature Trees for Solid Models. In: M.-S. Kim, K. Shimada (eds), Proc. Geometric Modeling and Processing, Springer LNCS, 4077:267-286, 2006. [DOI:10.1007/11802914_19] [PDF]
li2006
Approximate geometric models, e.g. as created by reverse engineering, describe the approximate shape of an object, but do not record the underlying design intent. Automatically inferring geometric aspects of the design intent, represented by feature trees and geometric constraints, enhances the utility of such models for downstream tasks. One approach to design intent detection in such models is to decompose them into regularity features. Geometric regularities such as symmetries may then be sought in each regularity feature, and subsequently be combined into a global, consistent description of the model’s geometric design intent. This paper describes a systematic approach for finding such regularity features based on recovering broken symmetries in the model. The output is a tree of regularity features for subsequent use in regularity detection and selection. Experimental results are given to demonstrate the operation and efficiency of the algorithm.
More Examples
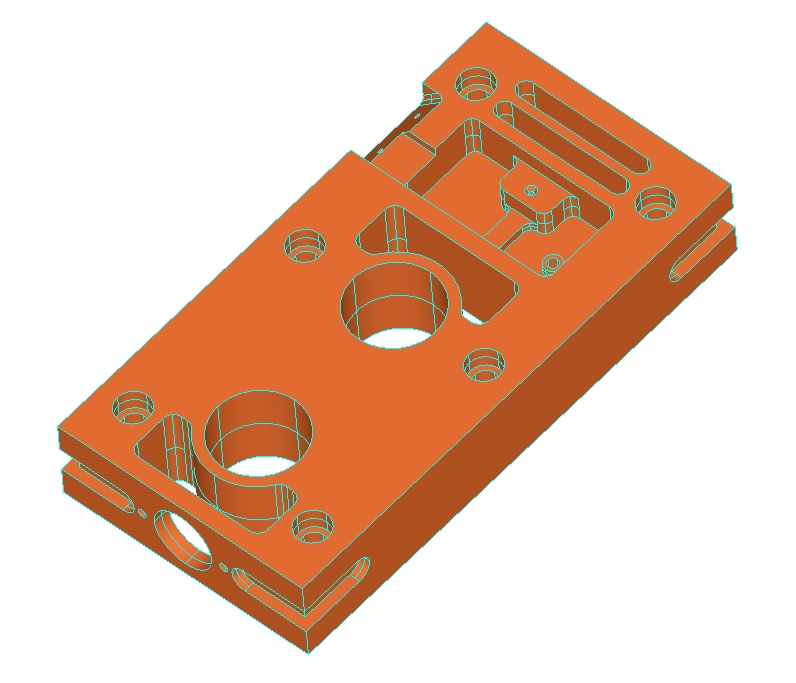
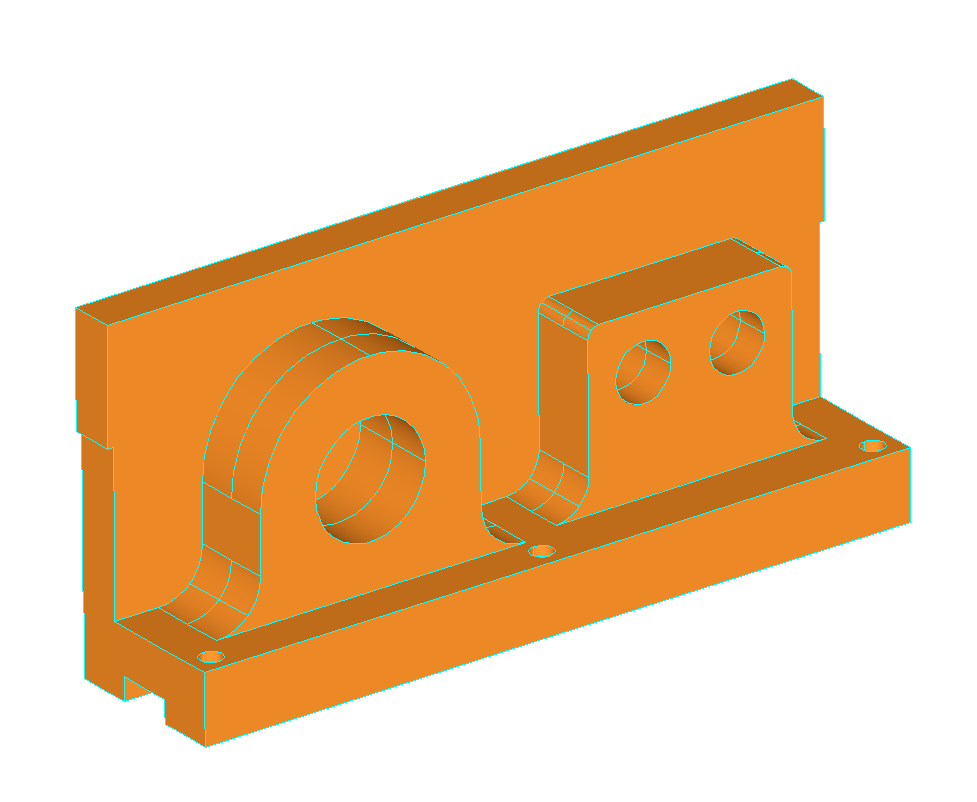
One approach to design intent detection in approximate geometric models is to decompose them into regularity features. Geometric regularities such as symmetries may then be sought in each regularity feature, and subsequently be combined into a global, consistent description of the model’s geometric design intent. Regularity feature tree decomposition is systematic approach for finding such regularity features based on recovering broken symmetries in the model. The resulting tree may be used subsequently in regularity detection and selection. Below are some examples of regularity feature tree (RFT) decompositions of geometric models for design intent detection. Click on the images to see the detailed decomposition results for each model. The RFT decomposition algorithm has been implemented under Linux using OpenCASCADE and experiments were run on a 3.4GHz Pentium 4E with 1GB RAM.
 |
 |
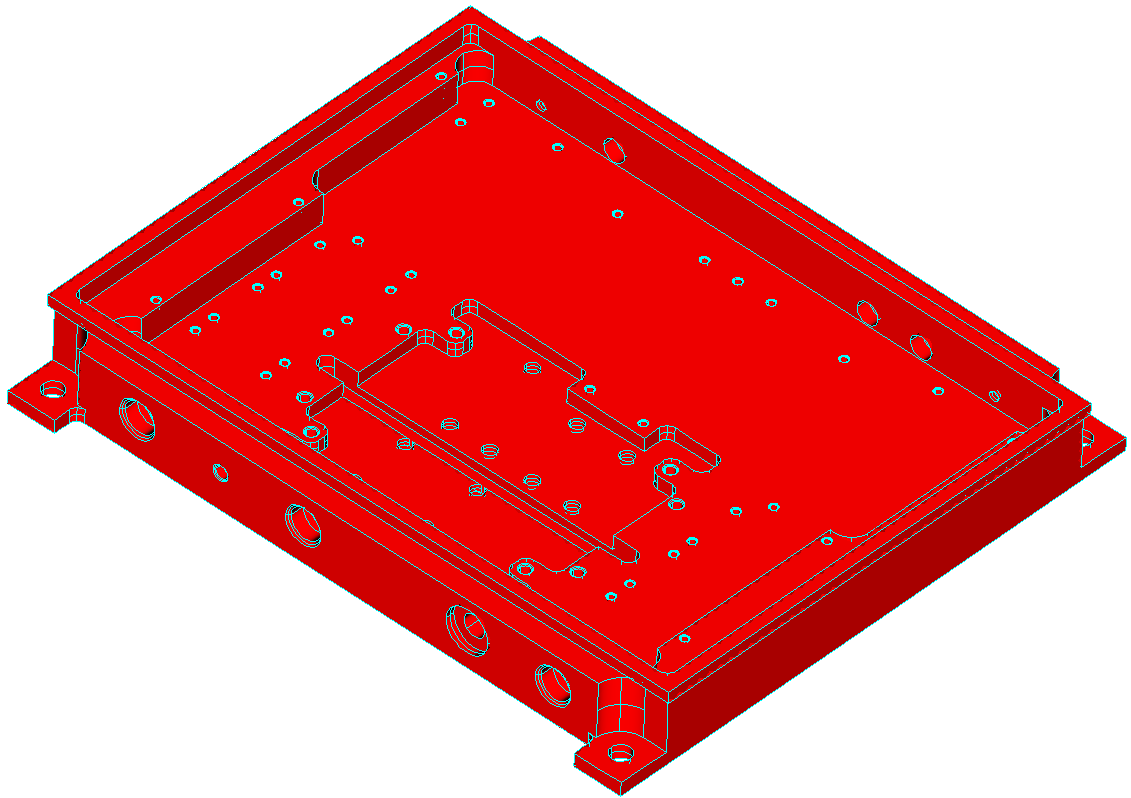| Monster | 2928056 |
 |
 |
| Team Part | VS TP |
 |
 |
| Clevis 22 | MOhne |
 |
|
| ISO14649 |
These models were derived from models available at the National Design Repository at Drexel University.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.